動画を使った錯視 13
2020年2月5日開設
警告: このページは本物の動画のページなので、長時間見続けないようにして下さい。ポケモン効果のようなフリッカー刺激は当然避けていますが、未知の危険要因もあるかもしれません。転載厳禁。

「一枚の画像から連続錯視拡大」
(色反転ナシ)
拡大して見える。
Copyright Akiyoshi Kitaoka 2020 (April 21)

「一枚の画像から連続錯視拡大」
拡大して見える。
Copyright Akiyoshi Kitaoka 2020 (April 20)

「一枚の画像から連続錯視拡大」
拡大して見える。
Copyright Akiyoshi Kitaoka 2020 (April 20)

「一枚の画像から連続錯視拡大」
(色反転ナシ)
拡大して見える。
Copyright Akiyoshi Kitaoka 2020 (April 21)

「一枚の画像から連続錯視回転」
反時計回りに回転して見える。
Copyright Akiyoshi Kitaoka 2020 (April 20)

(色反転ナシ)
Copyright Akiyoshi Kitaoka 2020 (April 21)

「一枚の画像から連続錯視拡大」
拡大して見える。
Copyright Akiyoshi Kitaoka 2020 (April 20)
-round02M-50ms.gif)
「reversed phi 形式の謎のファイ(右)のファイ部分だけでも普通のファイより動きが速く見える」
Copyright Akiyoshi Kitaoka 2020 (April 18)

(phenomenal phenomena 形式)

「reversed phi 形式の謎のファイ(右)は普通のファイより動きが速く見える」
Copyright Akiyoshi Kitaoka 2020 (April 17)

「phenomenal phenomena 形式の謎のファイ(右)は普通のファイより動きが速く見える」
Copyright Akiyoshi Kitaoka 2020 (April 17)


「リバースファイ(左)と謎のファイ(右)」
Copyright Akiyoshi Kitaoka 2020 (April 17)
すべての構成画像

---

「phenomenal phenomena形式のリバースファイ(左)と謎のファイ(右)」
Copyright Akiyoshi Kitaoka 2020 (April 17)

Thompson, P. (1982). Perceived rate of movement depends on contrast. Vision Research, 22, 377-380. Link


それぞれ、輝度コンテラストが高い左のリングは、輝度コンテラストの低い右のリングより、スピードは速く回転して見える、という予想となります。
Copyright Akiyoshi Kitaoka 2020 (April 14)
How do you see?
— Akiyoshi Kitaoka (@AkiyoshiKitaoka) April 14, 2020

「ローラー 2020」
ローラーが回転して見える
Copyright Akiyoshi Kitaoka 2020 (April 13)

「錯視的運動による大きさの錯視」
左の拡大して見える円は、右の縮小して見える円より小さく見える。
Copyright Akiyoshi Kitaoka 2020 (April 13)

(Matherタイプの変形)
「Four-stroke motion いろいろ」
リングの位置は静止しているが、リングは時計回りに回転して見える。
Copyright Akiyoshi Kitaoka 2020 (April 12)

(Mather タイプ)
(Mather タイプの変形)

(phenomenal phenomena)

(リバースファイ)

(リバースファイ new)
Copyright Akiyoshi Kitaoka 2020 (April 18)

(phenomenal phenomena)
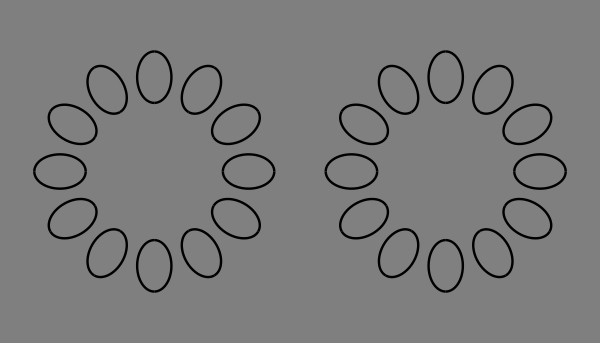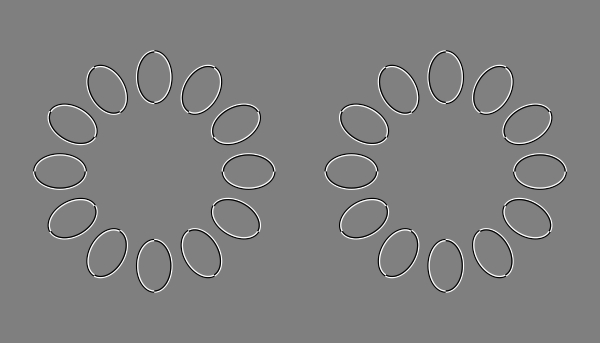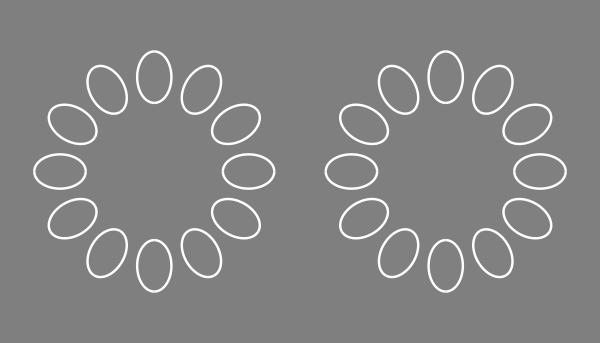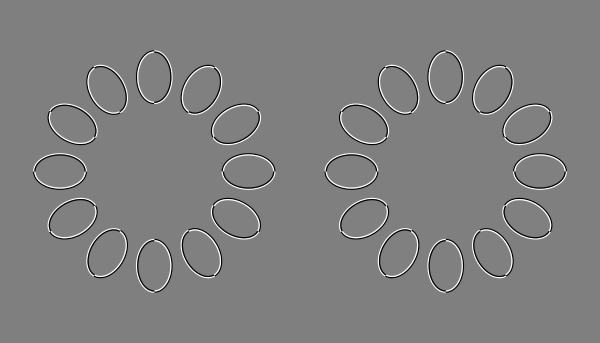
(局所的な手がかりによる全体の運動視)
(局所的な手がかりによる全体の運動視・リバースファイ風)
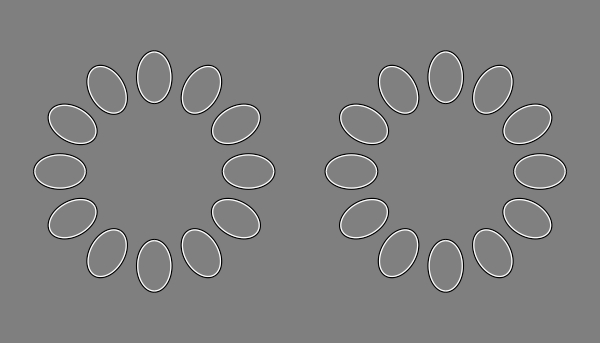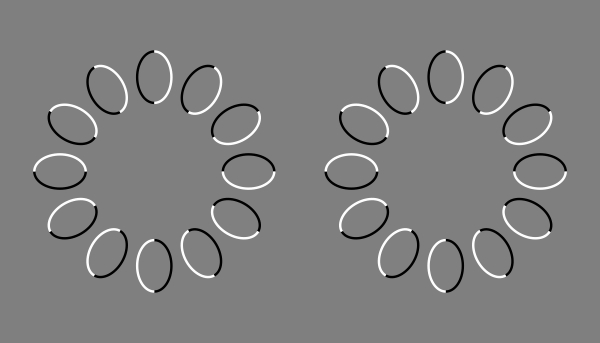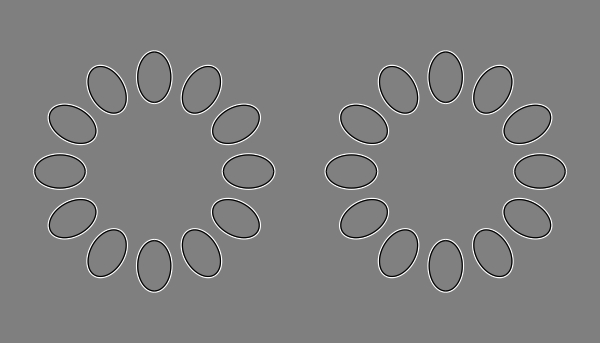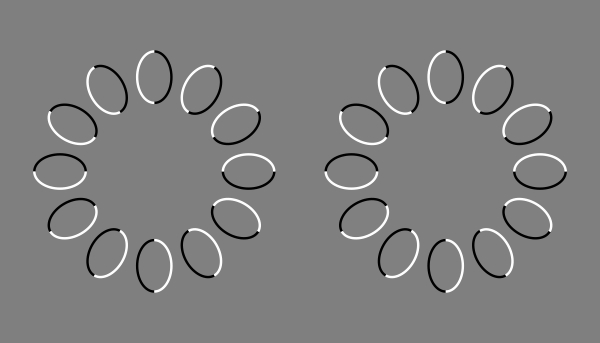
(局所的な手がかりによる全体の運動視・その2)

(局所的な手がかりによる全体の運動視・その2・リバースファイ風)

「錯視的運動による位置ズレの錯視」
The left ring appears to rotate counterclockwise while the right one to rotate clockwise, though they do not change their positions. Moreover, they are aligned vertically and horizontally, but the left ring appears to tilt counterclockwise slightly while the right one clockwise.
Copyright Akiyoshi Kitaoka 2020 (April 12)

「ファイ(?)とリバースファイ」
【タイトル】「リバース・リバースファイ」とでも言うべき運動刺激の現象観察
【刺激】左上と左下がテスト刺激で、中央と右の4つがコントロール刺激である。コントラスト極性の変化を伴う運動視について。左上は、リバースファイにならないように、回転するタイミングは同じ極性(黒→黒、白→白)としたもの。すなわち、極性が反転するフレーム間(黒→白、白→黒)では、リングの位置は変わらない。左下は、リバースファイが発生する条件で、極性が反転するフレーム間(黒→白、白→黒)において回転させ、同じ極性のフレーム間(黒→黒、白→白)では位置を変えない条件である。それらは2フレームおきに3度ずつ回転するが、リングの明るさを黒に固定あるいは白に固定して、2フレームおきに3度ずつ回転させたものが、中央の上と下のデモである。右の上下は、黒に固定あるいは白に固定のリングを1フレームごとに1.5度ずつ回転させたものである(左上の刺激は毎フレームごとに変化するので、変化の頻度という点でのコントロール刺激である)。位置の変化としては、6つのリングは互いに同じ角速度で回転するよう設計した。
【結果】左上の「ファイ」あるいは「リバース・リバースファイ」とでも言うべき刺激では、リングは反時計回りに回転して見えるが、中央と右の4つのリングよりも速く回転して見える。左下のリバースファイ入りの刺激では、反時計回りに回転して見えることがあるが、中央と右の4つのリングの回転と同程度か、遅く回転しているように見える。周辺視では時計回りに回転して見えることもある(リバースファイの効果)。
【考察】左上の「ファイ」あるいは「リバース・リバースファイ」とでも言うべき刺激は、コントロール刺激としたコントラスト極性の変化しない刺激よりも知覚される速度が速いことから、普通のファイ運動とは言えず、何か別の運動信号が加わっていると考えざるをえない。
【予想されるコメントと回答】
Q: リバースファイになっていないのではないか?
A: 本来のリバースファイ(オブジェクトだけでなく背景も輝度が変化する)のデモだとチカチカ度が高くて、SNSでデモするのはちょっと怖かったので、phenomenal phenomena 型のデモにしてあるが、同じことである。(ブツを出せ、と言われれば出します)
Q: チカチカすれば運動は加速して見えるということではないか?
A: リバースファイ(左下)の存在がそう単純でないことを示唆している。
Q: この現象は新しいのか?
A: 私は錯視研究が専門であるが、知覚心理学の教員なので、ある程度運動視も勉強はしているものの、網羅的に運動視の文献を見ているわけではないので、先行研究の有無については、現在のところ何とも言えない。私のFacebook友達にも運動視の研究者はいるので、何かコメントをくれるかもしれない。
Q: SNSで油売ってないで、論文書けよ。
A: そうですね。自宅謹慎いや自宅勤務とは言え、論文は書けますね~。複数の実験参加者のデータを取れ、と言われれば窮しますが。
https://www.facebook.com/akiyoshi.kitaoka/videos/10217868365635567/
Copyright Akiyoshi Kitaoka 2020 (April 11)

標準的リバースファイ版
Copyright Akiyoshi Kitaoka 2020 (April 21)
cf.

コントラスト極性の変化がないと、速度が速く見えるわけではないようだ。それどころか、中央の列の2つは遅く見える。(下図参照)
Copyright Akiyoshi Kitaoka 2020 (April 22)


100 ms / frame

70 ms / frame

50 ms / frame
左右のリングは同じ角速度で回転させているが、左のリングの回転は周辺視では遅く見える。
Copyright Akiyoshi Kitaoka 2020 (April 22)

500 ms / frame

(4 frames)
Copyright Akiyoshi Kitaoka 2020 (April 11)

(reversed phi: 4 frames, 80 ms / frame)

「ファイ(?)の速度過大視?」
左右のリングは反時計回りに同じ速度で回転しているが、右のリングは左のリングよりも速く回転して見える。
Copyright Akiyoshi Kitaoka 2020 (April 8)
![]()
http://crowding.github.io/thesis/
Ⓒ 2014 Peter Meilstrup (Twitter | Github)
<April 4, 2020>
![]()
Rotating Reversals
Ⓒ 2008 Arthur Shapiro

<April 30, 2020>

4 frames; 150 ms / frame
「収縮活動(略して、収活)
この動画は4枚の画像でできていて、同心円は同じ位置にあるが、収縮しているように見える。
Copyright Akiyoshi Kitaoka 2020 (April 3)

8 frames; 70 ms / frame
Copyright Akiyoshi Kitaoka 2020 (April 4)

4 frames; 150 ms / frame
Copyright Akiyoshi Kitaoka 2020 (April 4)

4 frames; 150 ms / frame
「拡大活動」
この動画は4枚の画像でできていて、同心円は同じ位置にあるが、拡大しているように見える。
Copyright Akiyoshi Kitaoka 2020 (April 3)

8 frames; 70 ms / frame
Copyright Akiyoshi Kitaoka 2020 (April 4)

4 frames; 150 ms / frame
Copyright Akiyoshi Kitaoka 2020 (April 4)

50 ms/frame
「電車のシーンの8ストローク運動(すべてリバースファイ)デモ」
(反転画像は、オリジナルフレームのネガポジ反転)
この動画はたった8枚の画像でできているが、電車は常に進行しているように見える。
Copyright Akiyoshi Kitaoka 2020 (March 22)


50 ms/frame
(反転画像は、オリジナル動画の2フレーム目)
Copyright Akiyoshi Kitaoka 2020 (March 22)

50 ms/frame
「電車のシーンの16ストローク運動(すべてリバースファイ)デモ」
(反転画像は、オリジナル動画の2フレーム目)
この動画は16枚の画像でできているが、電車は常に進行しているように見える。
Copyright Akiyoshi Kitaoka 2020 (March 22)

100 ms /frame
「電車のシーンの4ストローク運動(すべてリバースファイ)デモ」
(反転画像は、オリジナルフレームのネガポジ反転)
この動画はたった4枚の画像でできているが、電車は常に進行しているように見える。
Copyright Akiyoshi Kitaoka 2020 (March 22)

80 ms /frame
(反転画像は、オリジナル動画の2フレーム目)
Copyright Akiyoshi Kitaoka 2020 (March 22)

80 ms/frame
「電車のシーンの(マーザーの)4ストローク運動デモ」
この動画はたった4枚の画像でできているが、電車は常に進行しているように見える。
Reference: http://www.georgemather.com/MotionDemos/FourstrokeMP4.html
Copyright Akiyoshi Kitaoka 2020 (March 12)
Differences in perceived speed pic.twitter.com/bwOeeAnKV8
— Akiyoshi Kitaoka (@AkiyoshiKitaoka) March 11, 2020

100 ms/frame

「電車のシーンのリバースファイ運動デモ」
この動画は3枚の画像でできていて、絵としては後退するように配置しているのだが、電車は進行しているように見える。
Copyright Akiyoshi Kitaoka 2020 (March 13)
Differences in perceived speed pic.twitter.com/V42VxQDRZ3
— Akiyoshi Kitaoka (@AkiyoshiKitaoka) February 4, 2020
「知覚速度自由自在2020」
電車の進行方向をビデオカメラで見ている時、ズームすると走行速度が遅く見え、広角にすると走行速度が速く見える。
Copyright Akiyoshi Kitaoka 2020 (February 4)
cf. 同心円状で対数的配置のサイン波状輝度格子の拡大運動 (1 Hz; '拡大率' = 1.414 (left) and 2 (right))

