多義図形・反転図形 7
since July 27, 2014

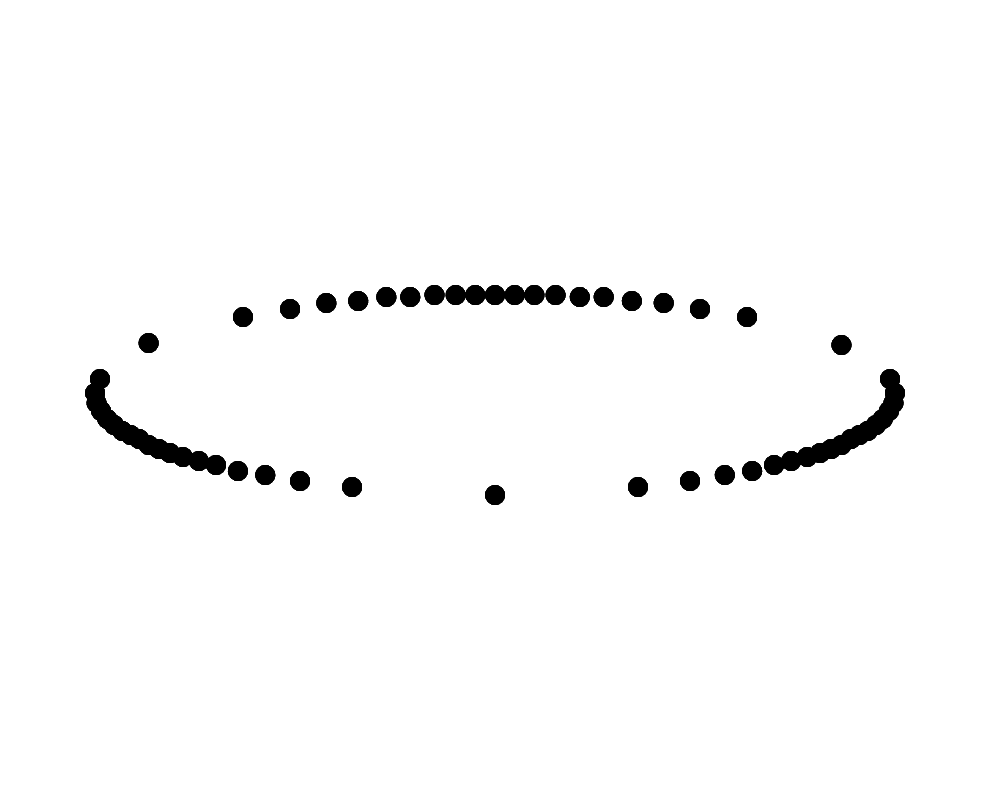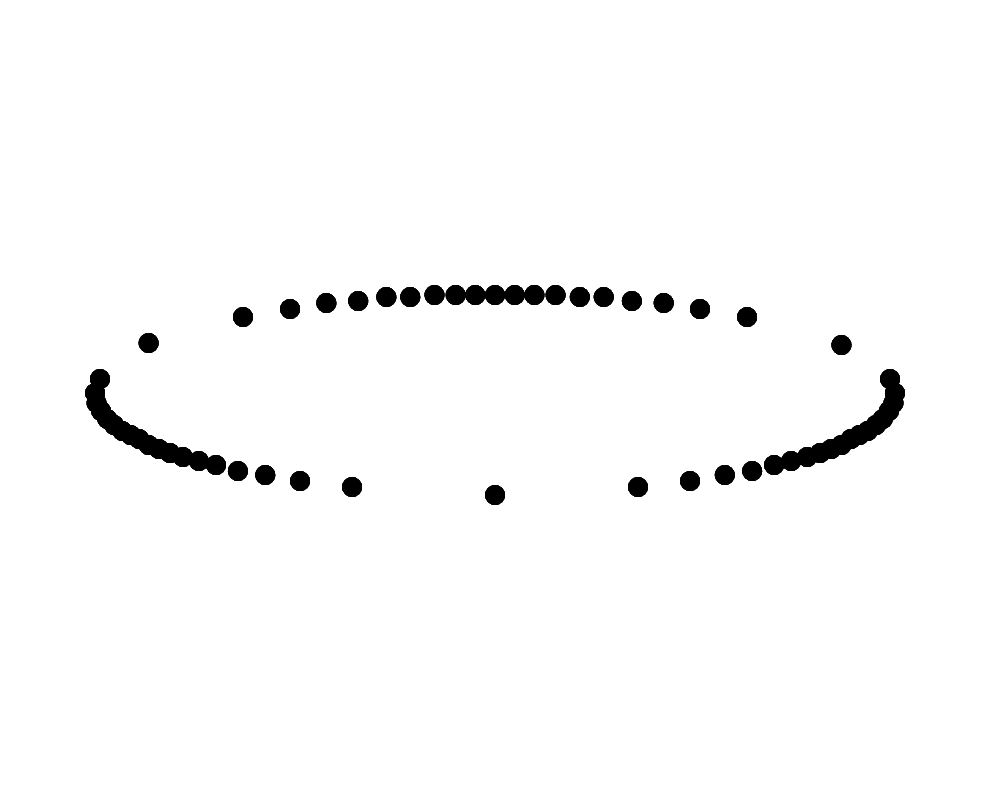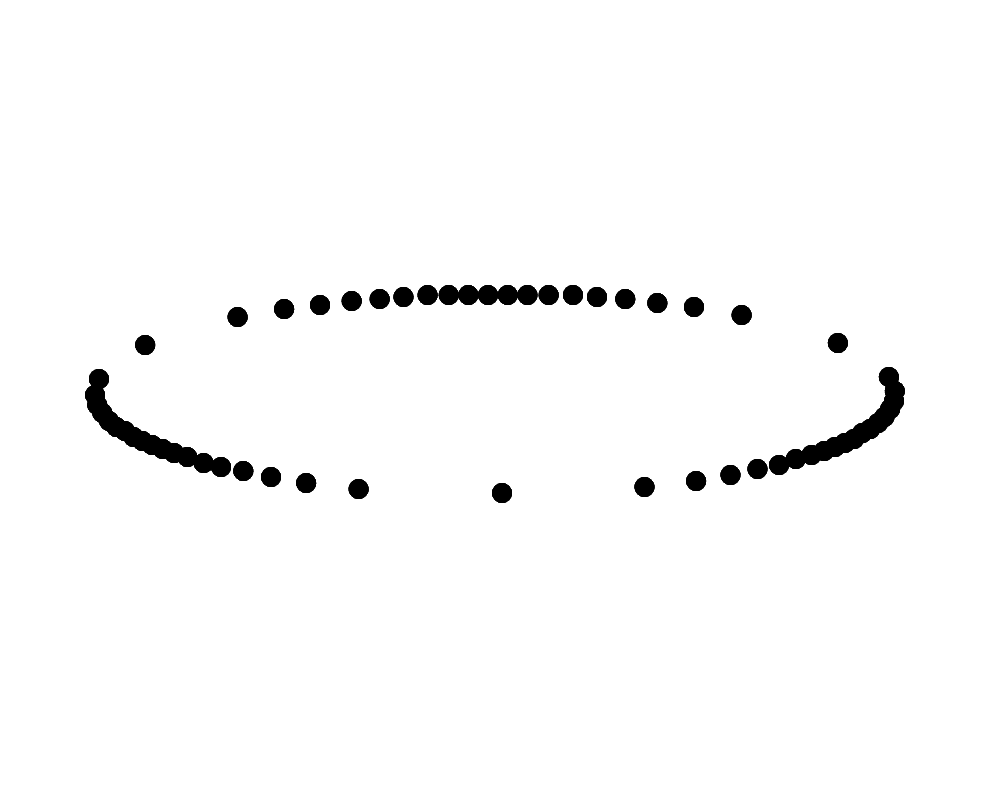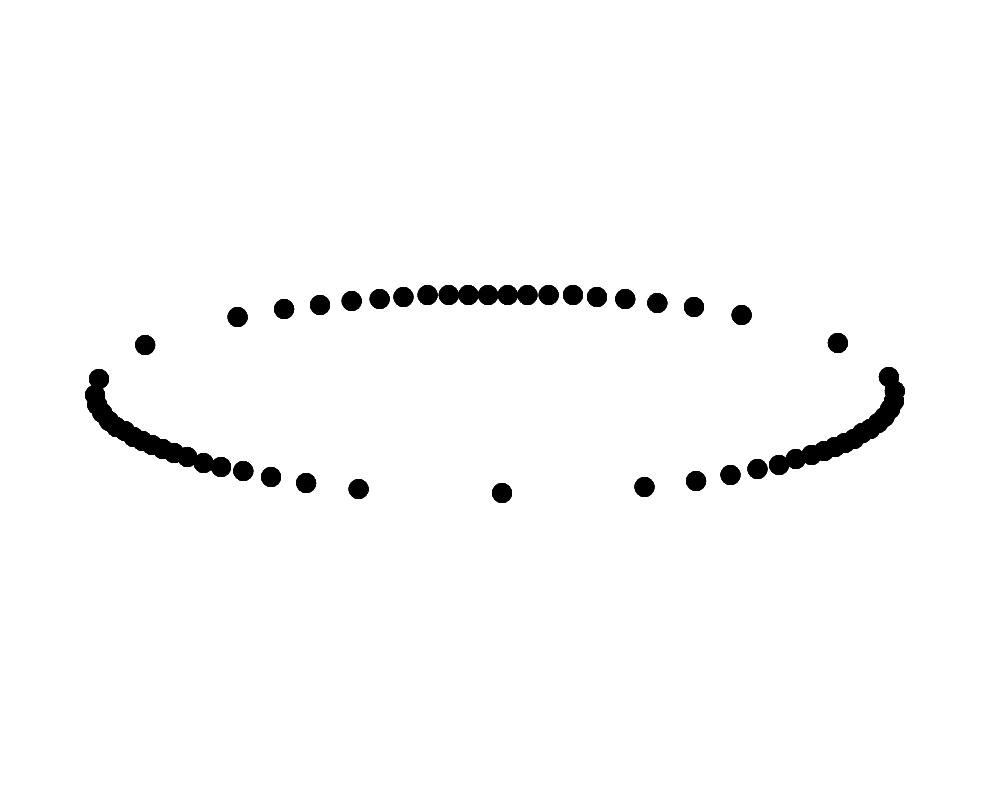
斜め上から見下ろして時計回りに回転して見えるリングに見えるか、斜め下から見上げて時計回りに回転して見えるリングに見える。
Copyright Akiyoshi Kitaoka 2023 (July 12)
斜め上から見下ろして反時計回りに回転して見えるリングに見えるか、斜め下から見上げて反時計回りに回転して見えるリングに見える。
Copyright Akiyoshi Kitaoka 2023 (July 12)
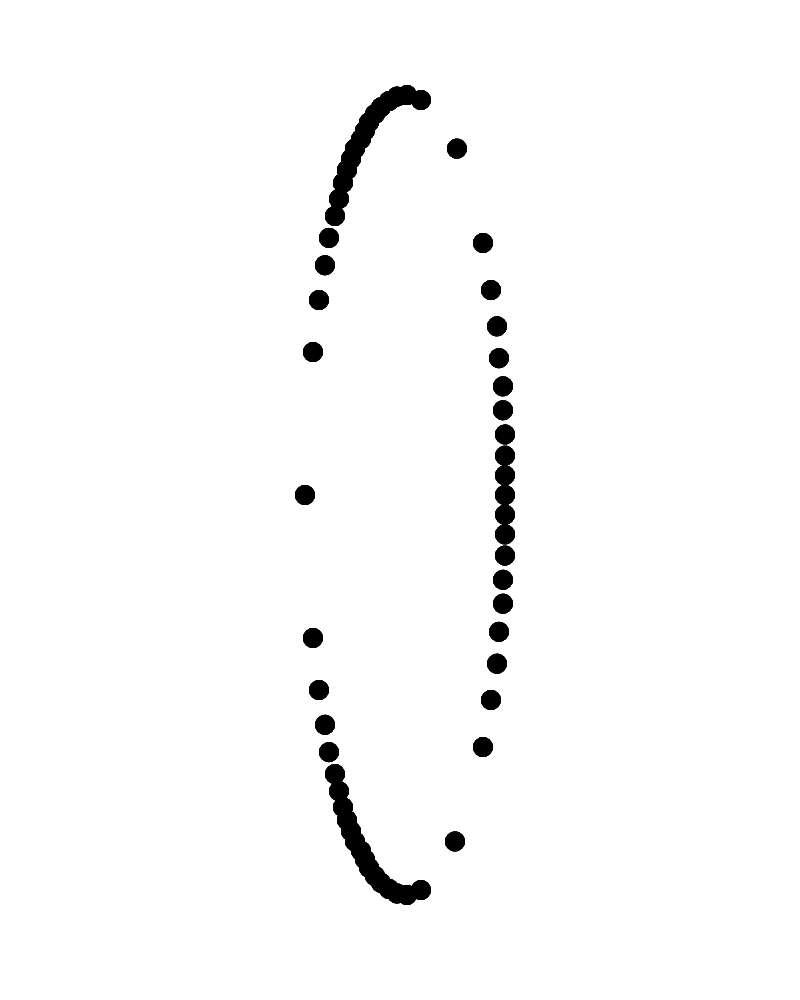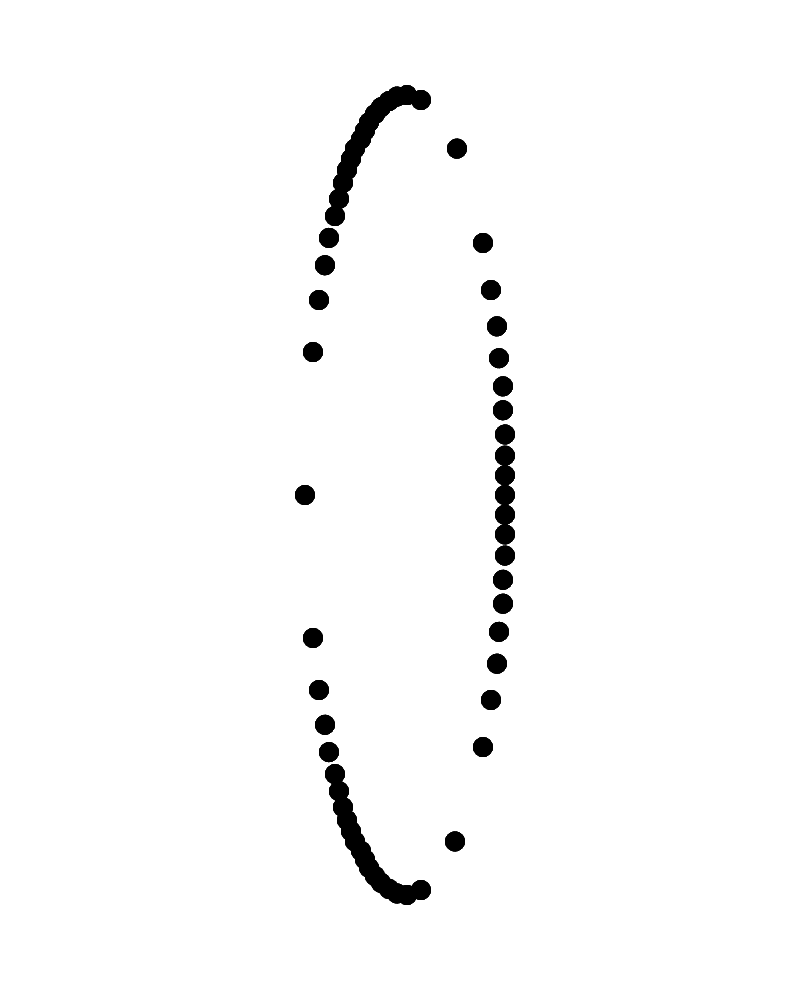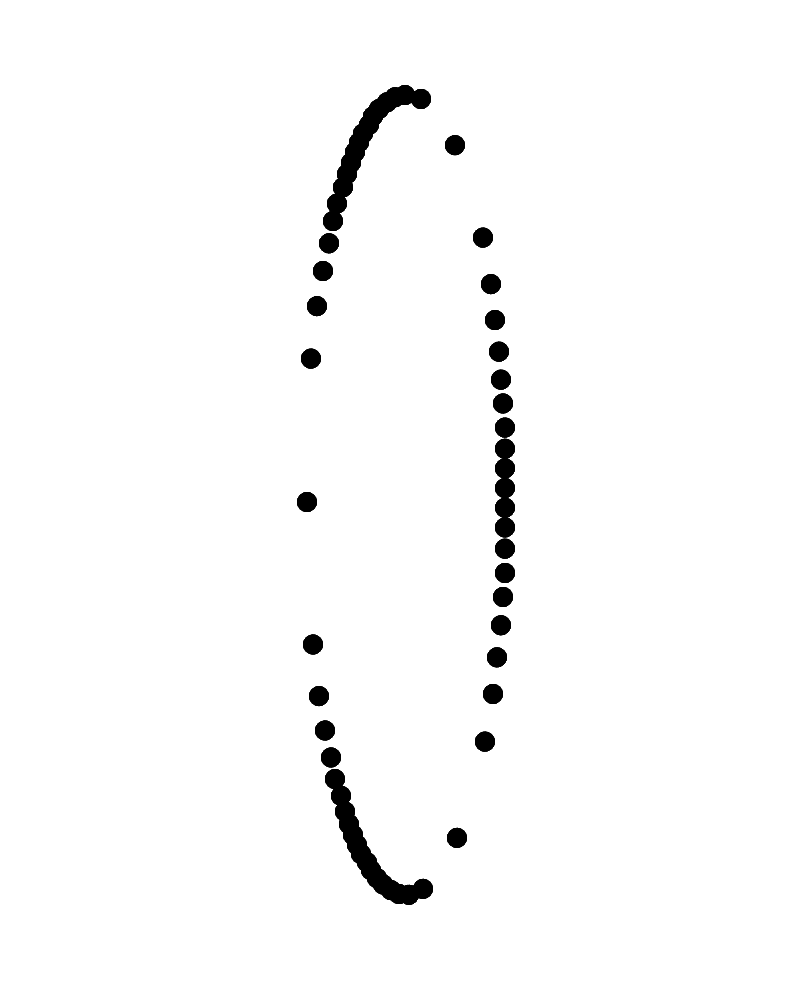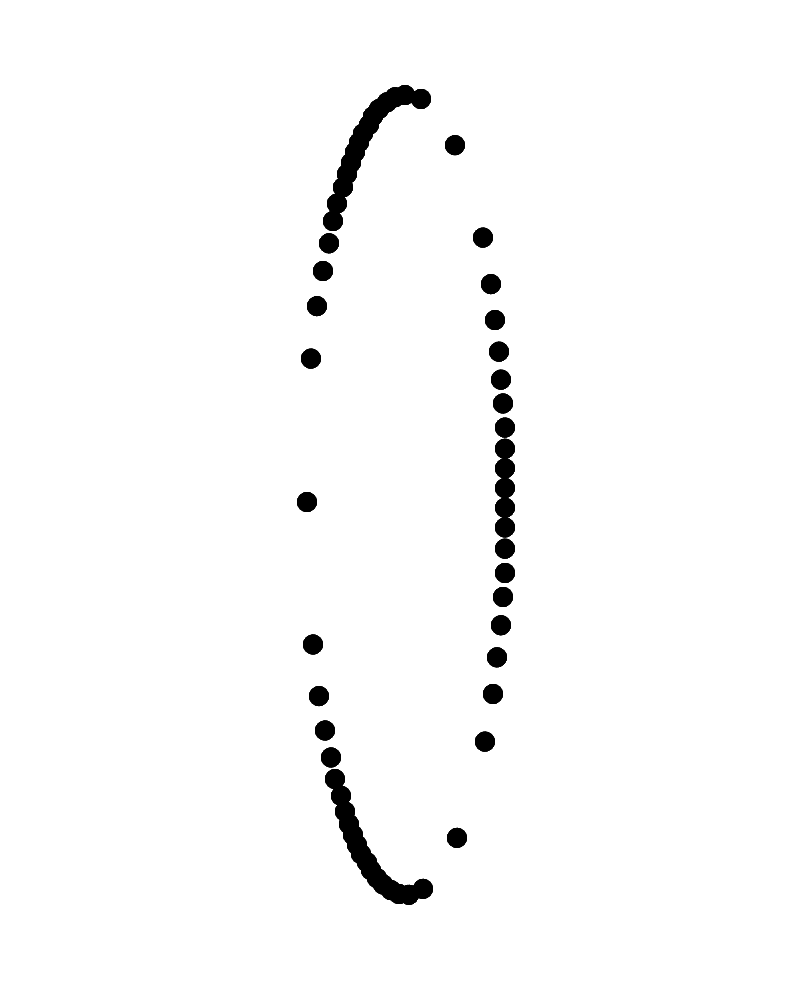
右側が手前に左側が奥に見えて時計回りに回転して見えるリングに見えるか、左側が手前に右側が奥に見えて時計回りに回転して見えるリングに見える。
Copyright Akiyoshi Kitaoka 2023 (July 13)
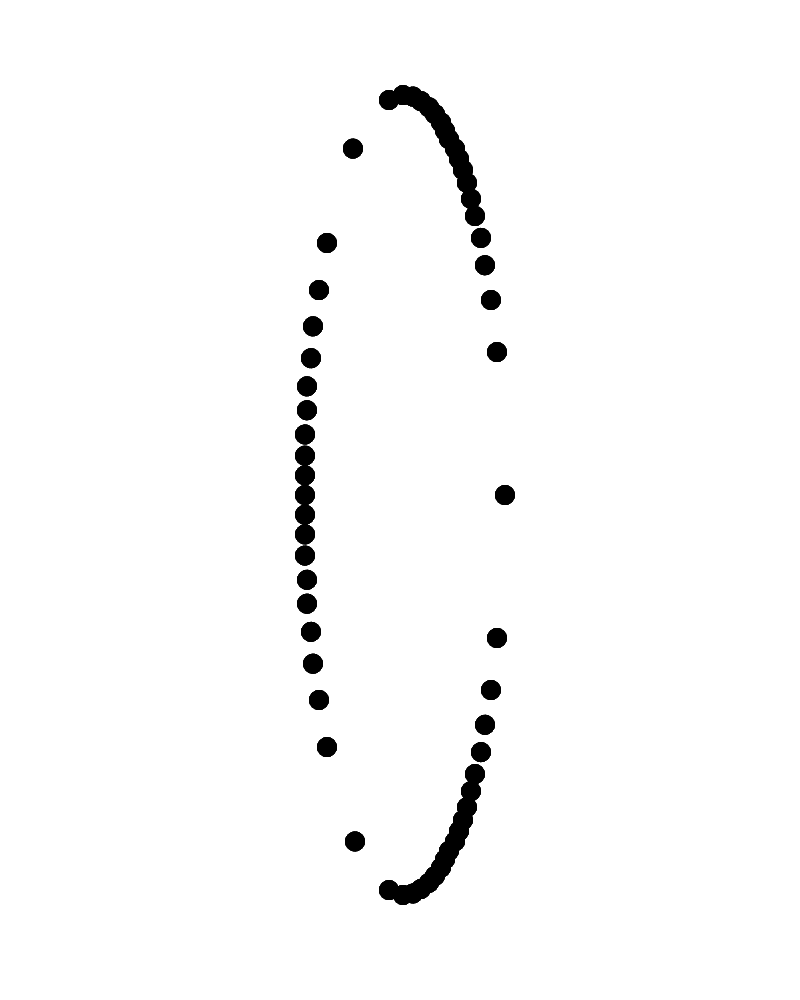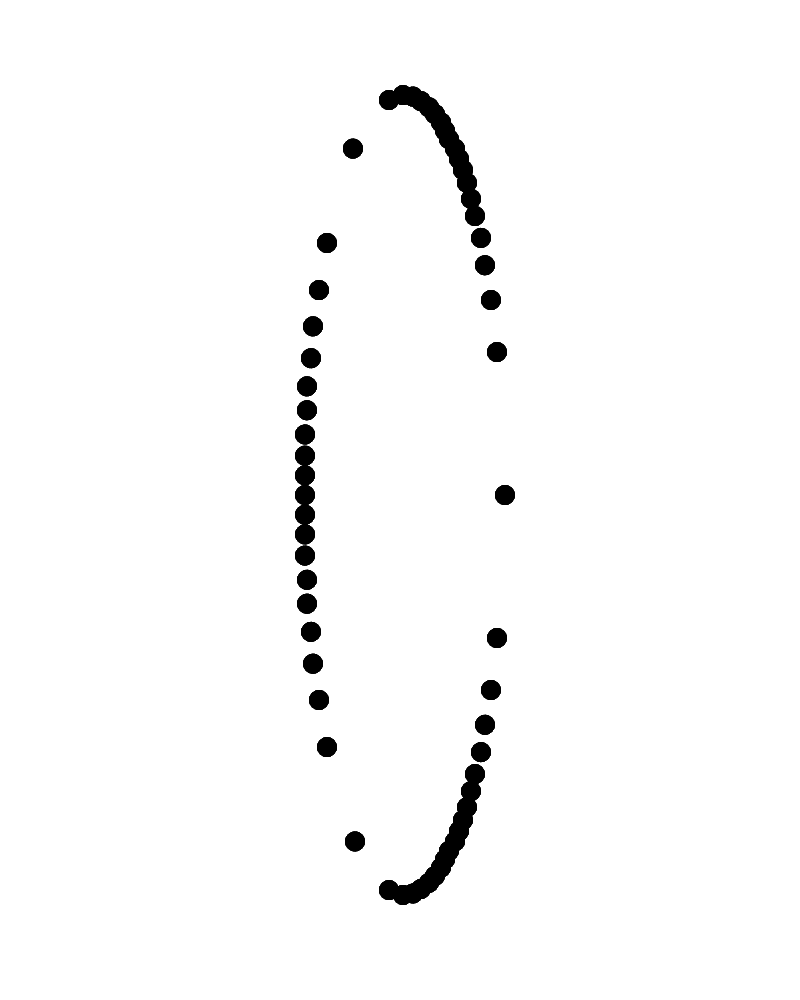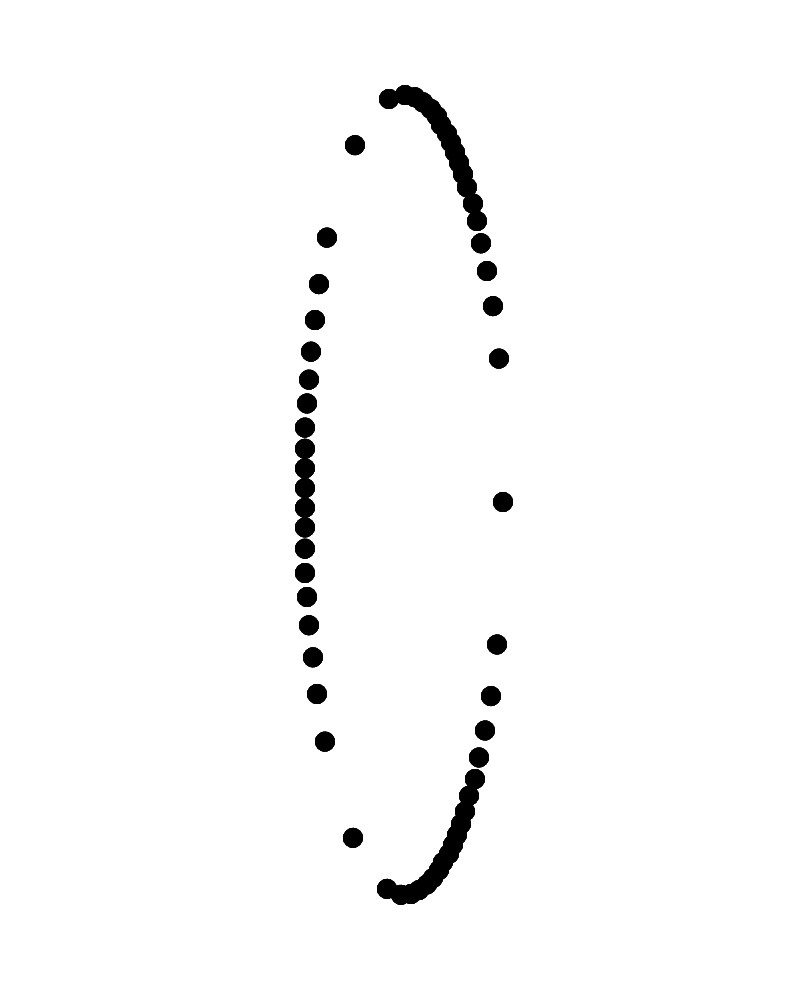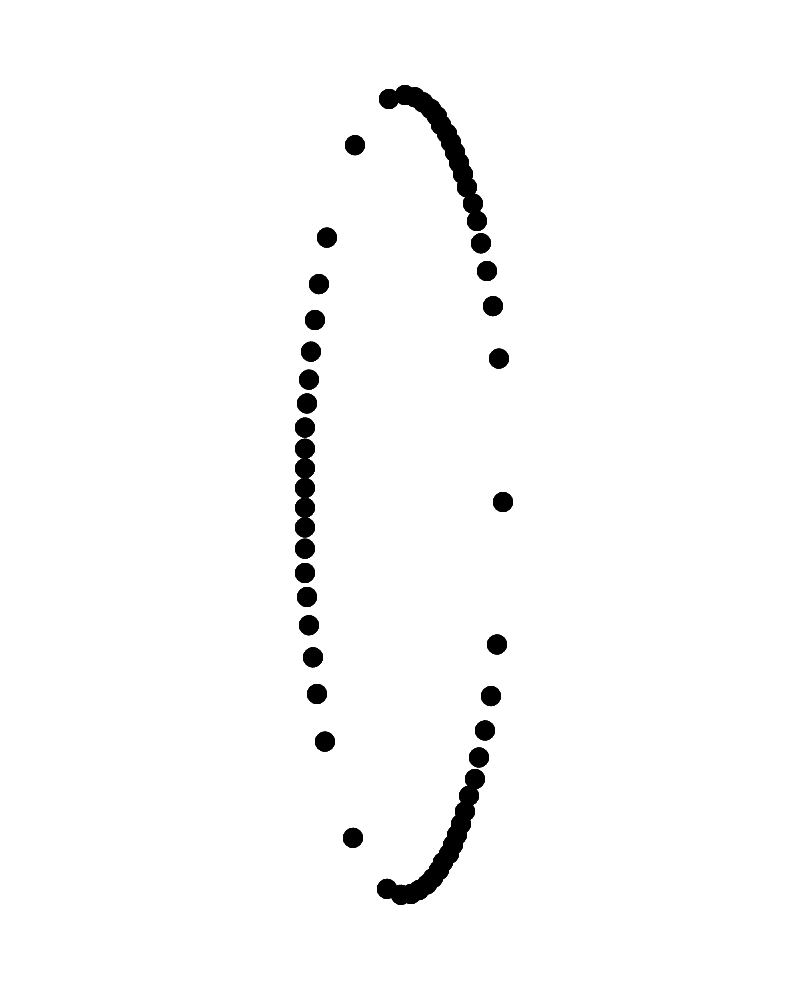
右側が手前に左側が奥に見えて反時計回りに回転して見えるリングに見えるか、左側が手前に右側が奥に見えて反時計回りに回転して見えるリングに見える。
Copyright Akiyoshi Kitaoka 2023 (July 13)

上から見下ろして時計回りに回転して見えるリングに見えるか、下から見上げて時計回りに回転して見えるリングに見える。
Copyright Akiyoshi Kitaoka 2023 (August 18)
Which is predominant?
— Akiyoshi Kitaoka (@AkiyoshiKitaoka) July 5, 2023
For me, the clockwise rotation is predominant. I guess it's a 50-50 split, but is it correct? Could you vote which is predominant for you?
— Akiyoshi Kitaoka (@AkiyoshiKitaoka) July 7, 2023
Copyright Akiyoshi Kitaoka 2023 (July 7)
Copyright Akiyoshi Kitaoka 2023 (July 7)

「奥行き反転図形のビンとカン」
ビンとカンの奥行きが反転して見える。立命館大学大阪いばらきキャンパスにて撮影。
Copyright Akiyoshi Kitaoka 2017 (March 10)

「立命館慶祥高等学校多義図形」
「立命館慶祥高等学校」と書かれた白い部分は上下で一致しているが、上の図ではそれは右下を向いているように見え、下の図では左上を向いているように見える。
Copyright Akiyoshi Kitaoka 2014 (September 26)

「京都アスニー多義図形」
「京都アスニー」と書かれた白い部分は上下で一致しているが(青い枠の中においても一致)、上の図でそれは下方を向いているように見え、下の図では上方を向いているように見える。
Copyright Akiyoshi Kitaoka 2014 (September 17)

「平行四辺形は奥行反転図形」
Copyright Akiyoshi Kitaoka 2014 (September 17)
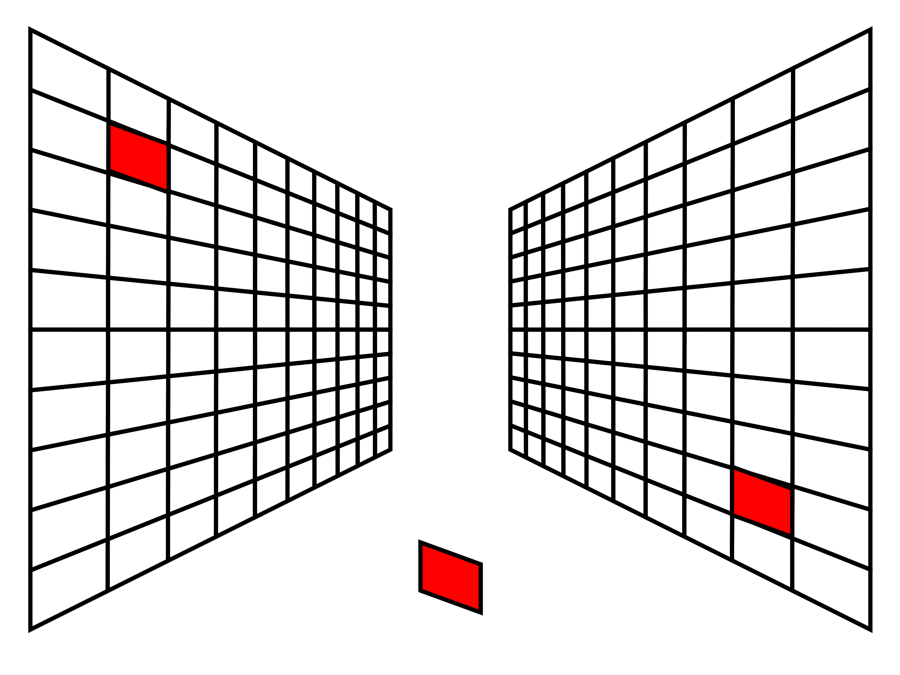
「平行四辺形の場合の形の恒常性」
(平行四辺形は奥行反転図形の説明図 1)
Copyright Akiyoshi Kitaoka 2014 (September 18)
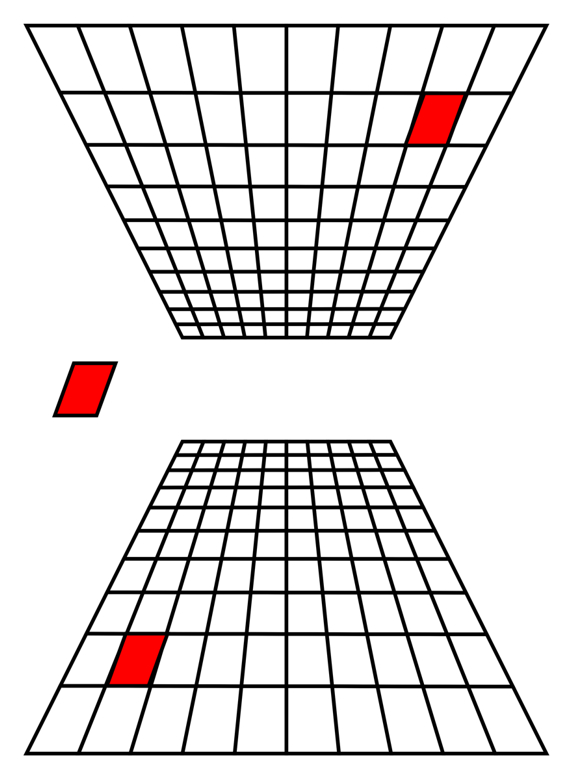
「平行四辺形の場合の形の恒常性 2」
(平行四辺形は奥行反転図形の説明図 2)
Copyright Akiyoshi Kitaoka 2014 (September 18)
●形の恒常性

北岡明佳(編著) (2011) いちばんはじめに読む心理学の本⑤ 知覚心理学 ―心の入り口を科学する― ミネルヴァ書房 amazon (2011年4月刊、総ページ数は297ページ) 北岡執筆部分の図一覧
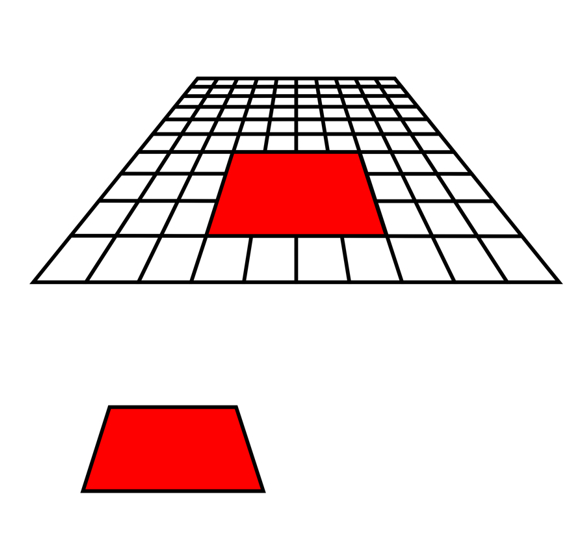
「台形の場合の形の恒常性」
Copyright Akiyoshi Kitaoka 2014 (September 18)
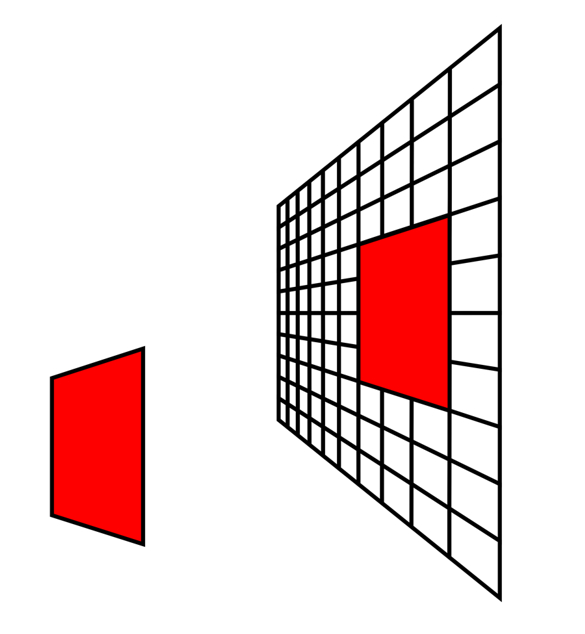
「台形の場合の形の恒常性 2」
Copyright Akiyoshi Kitaoka 2014 (September 18)
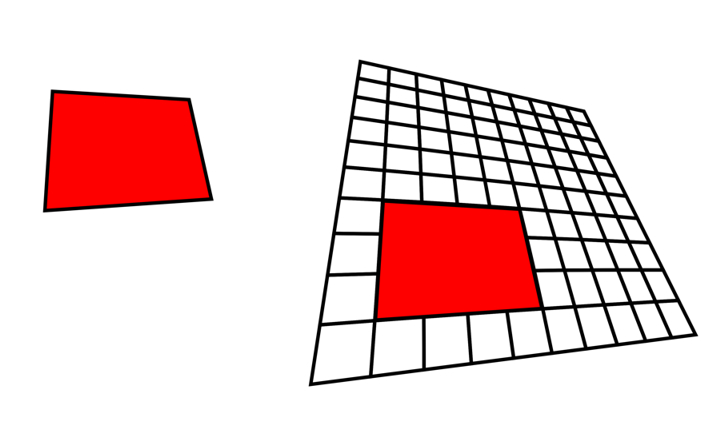
「不等辺四辺形の場合の形の恒常性」
Copyright Akiyoshi Kitaoka 2014 (September 18)
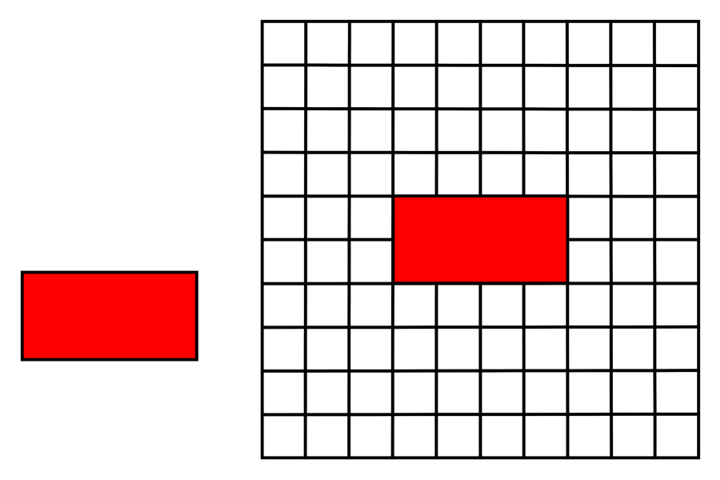
「長方形の場合の形の恒常性」
Copyright Akiyoshi Kitaoka 2014 (September 18)

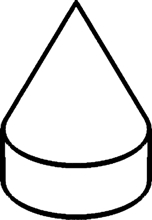
「ケーキとロケット」
after Fig. 4.2 of Barrow and Tenenbaum (1981)
reproduced by Tadamasa Sawada
Barrow, H. G. and Tenenbaum, J. M. (1981). Interpreting line drawings as three-dimensional surfaces. Artificial Intelligence, 17, 75–116. (p. 86, FIG. 4. 2.)
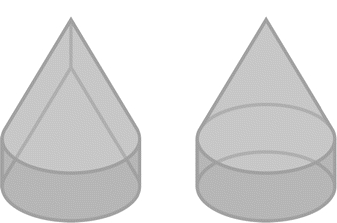
「ケーキとロケット:それぞれ上から見たところと下から見たところ」
after Figure 2 of Tsuruhara, Sawada, Kanazawa, Yamaguchi, Corrow and Yonas (2010)
reproduced by Tadamasa Sawada
Tsuruhara, A., Sawada, T., Kanazawa, S., Yamaguchi, M.K., Corrow, S., and Yonas, A. (2010). The development of the ability of infants to utilize static cues to create and access representations of object shape. Journal of Vision, 10(12), article 2; http://www.journalofvision.org/content/10/12/2 doi: 10.1167/10.12.2 (p.3, the lower part of Figure 2)
with permission on July 24, 2014