ステレオグラム 4
・3つ並んだ図の場合は左と中の図あるいは中と右の図を両眼融合させて見ることができます。たくさん並んだ図の場合は隣合った図を合わせてください。このようなフリーフューズはできない人が多いですが、練習がモノを言います。それでもできない人もいますが、知能・学力等とは一切関係ありません。
2009年6月18日より

「両眼立体視的に奥行き方向に傾いた辺の過大視」
隣同士を両眼融合すると、斜辺は奥行き方向に傾いて見える。その時、描かれた絵としては斜辺は上辺・下辺よりも若干短い(上辺・下辺を100とすると、左端と右端の平行四辺形の斜辺は約93.6、中央の平行四辺形の斜辺は約97.3)が、斜辺は上辺と下辺よりも長く見える。これは、「両眼立体視的シェパード錯視」といったところである。
そのほか、両眼融合すると、上辺と下辺の長さは異なって見える(遠くに見えるものは近くに見えるものと比較して網膜像が大きく見える現象で、「(両眼立体視的)大きさの恒常性」*と呼ばれることがある)。これに伴ってなのか、こちらが原因なのか、物理的には平行な斜辺が平行でなく見える。具体的には、奥に向かって開散する方向に角度がついて見える。これは、「両眼立体視的斜塔錯視」といったところである。
*「大きさの恒常性」(size constancy)は、一般的には、対象までの距離に依存して対象が映る網膜像の大きさ(近刺激の大きさ)が変化しても、対象の「本当の大きさ」(知覚された遠刺激の大きさ)は一定に見えることを指す。であるから、目に映った大きさを評価させると、遠くにある対象は小さく見え、近くにある対象は大きく見えている。一方、「(両眼立体視的)大きさの恒常性」は遠くにある対象が近くの対象に比べて少し大きく見える現象である(遠くの対象の知覚された近刺激が、近くの対象の知覚された近刺激より相対的に大きく見える)。つまり、両者は違う現象なのであるが、ともに「大きさの恒常性」と呼ばれることが多いのでまぎらわしい。前者(一般的な意味での大きさの恒常性)は機能的である(目に映る対象の像の大きさが変わったからといって対象が実際に大きくなったり小さくなったりすると知覚しない方が「正しい」)が、後者(両眼立体視的な大きさの恒常性)はいわば錯視的である(遠くの対象が少し大きく見える必要性が明確でない)。
Copyright Akiyoshi Kitaoka 2010 (December 17)
cf. Thouless, R. H. (1931) Phenomenal regression to the real object. I. British Journal of Psychology, 21, 339-359. <2011年2月26日追記>
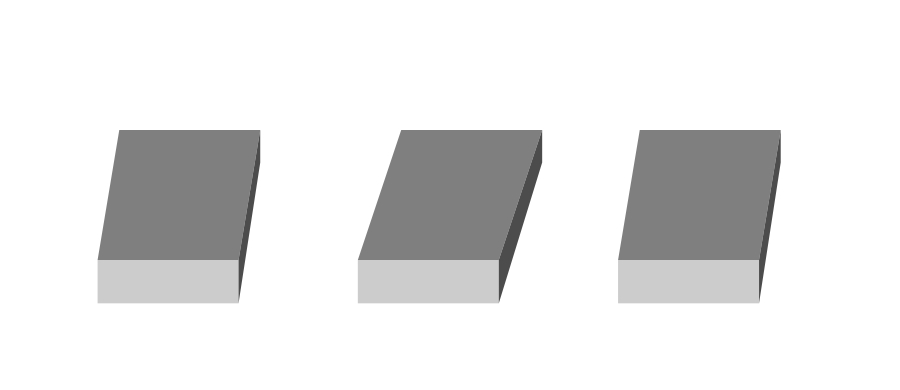
「シェパード錯視と、両眼立体視的に奥行き方向に傾いた辺の過大視」
物理的には、斜辺は上辺・下辺よりも若干短い(上辺・下辺を100とすると、左端と右端の平行四辺形の斜辺は約93.6、中央の平行四辺形の斜辺は約97.3)が、斜辺は上辺と下辺と同じかむしろ長く見える。これは、「シェパード錯視」である。
隣同士を両眼融合すると、斜辺は奥行き方向に傾いて見える。その時、斜辺は上辺と下辺よりも長く見える。これは、「シェパード錯視と、両眼立体視的に奥行き方向に傾いた辺の過大視の合成」といったところである。
そのほか、両眼融合すると、上辺と下辺の長さは異なって見える(遠くに見えるものは近くに見えるものと比較して網膜像が大きく見える現象で、「大きさの恒常性」と呼ばれることがある)。これに伴ってなのか、こちらが原因なのか、物理的には平行な斜辺が平行でなく見える。具体的には、奥に向かって開散する方向に角度がついて見える。これは、「両眼立体視的斜塔錯視」といったところである。
Copyright Akiyoshi Kitaoka 2010 (December 17)
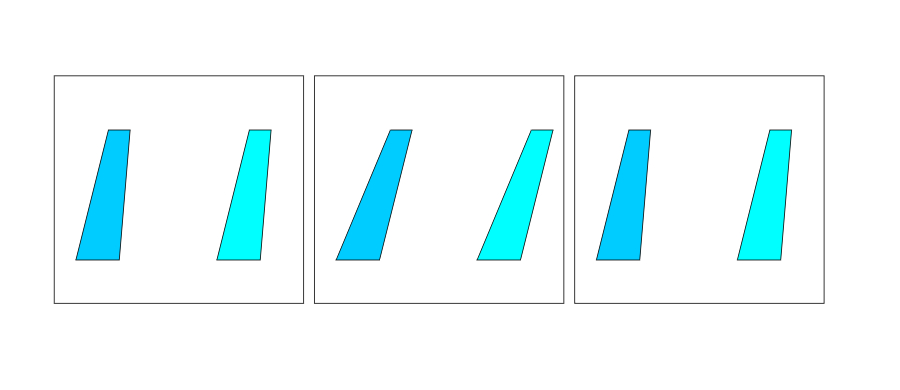
「両眼立体視的斜塔錯視」
枠内の2つの台形は同じ形で平行に並んでいるが、右側の方がより時計回りに傾いて見える(斜塔錯視)。両眼立体視して上辺が奥に見える場合、斜塔錯視が強められる。上辺が手前に見える場合は、斜塔錯視は弱くなる。
Copyright Akiyoshi Kitaoka 2010 (December 17)

「両眼立体視的長(おさ)錯視」
各台形の斜辺の成す角度は90度である。しかし、隣同士両眼融合すると過小視されて、かなり鋭角に見える。上辺が奥に見える場合に特に顕著である。「両眼立体視的に奥行き方向に傾いた辺の過大視」との関係が示唆される。
Copyright Akiyoshi Kitaoka 2010 (December 17)

「長(おさ)錯視と両眼立体視的長(おさ)錯視」
それぞれの青い道路の台形の斜辺の成す角度は90度であるが、鋭角に見える(長錯視あるいは道路写真の角度錯視)。しかし、隣同士両眼融合するとさらに過小視されて、かなり鋭角に見える。上辺が奥に見える場合に特に顕著である。
Copyright Akiyoshi Kitaoka 2010 (December 17)
Thanks to Idesawa sensei for discussion

「両眼立体視的長(おさ)錯視・Xmas版」
各台形の斜辺の成す角度は90度である。しかし、隣同士両眼融合すると過小視されて、かなり鋭角に見える。上辺が奥に見える場合に特に顕著である。「両眼立体視的に奥行き方向に傾いた辺の過大視」との関係が示唆される。単眼でも台形の斜辺の成す角度が鋭角に見えれば、それは長錯視である。
Copyright Akiyoshi Kitaoka 2010 (December 17)
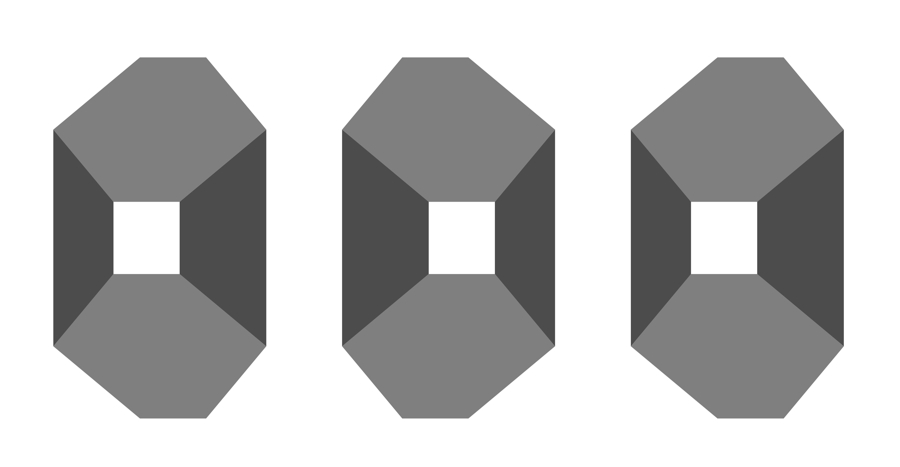
「両眼立体視的長(おさ)錯視・鈍角版」
隣同士両眼融合して観察すると、床あるいは天井の左右の折れ曲がった辺の成す角は絵では90度なのにそれより大きく見える。
Copyright Akiyoshi Kitaoka 2010 (December 19)

「長(おさ)錯視・鈍角版」
道路の左右の折れ曲がった辺の成す角は絵では90度なのにそれより大きく見える。
Copyright Akiyoshi Kitaoka 2010 (December 20)

「フレーザー錯視のステレオグラム」
隣ずつねじれひもを両眼融合すると、局所的斜線のみ奥行き方向に傾いて見え、全体的に奥行き方向に傾いて見えるということはない。
Copyright Akiyoshi Kitaoka 2010 (August 6)

「透明視的パヌムの限界条件・四重像」
両眼融合すると、奥行きの異なる4つの像が見える。 2×2=4 ?
Copyright Akiyoshi Kitaoka 2009 (July 1, 7)
4層に見えない人のために、奥行き面を赤円で示した。↓


「透明視的パヌムの限界条件・三重像」
両眼融合すると、奥行きの異なる3つの像が見える。
Copyright Akiyoshi Kitaoka 2009 (June 29, July 1)
 顔ガクガク錯視ぢゃないんだよ。
顔ガクガク錯視ぢゃないんだよ。

「透明視的パヌムの限界条件」
両眼融合すると、奥行きの異なる2つの画像が見える。
Copyright Akiyoshi Kitaoka 2009 (June 29)
 中溝幸夫先生によると、パヌムの限界条件の説明には二重融合仮説(double-fusion hypothesis)はダメなのだそうであるが、本図はそれでしか説明できないような気がするなあ・・・
中溝幸夫先生によると、パヌムの限界条件の説明には二重融合仮説(double-fusion hypothesis)はダメなのだそうであるが、本図はそれでしか説明できないような気がするなあ・・・
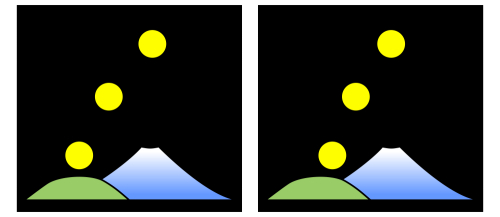
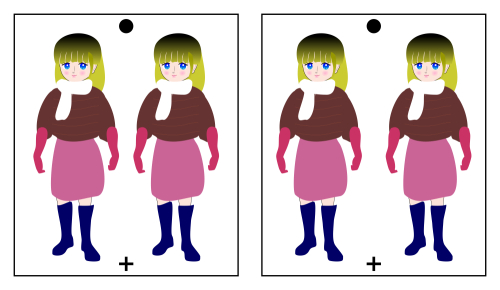
「両眼立体視による大きさの恒常性のデモ」
網膜像としては同じ大きさのものでも、相対的に遠くに見えるものは大きく見え、近くに見えるものは小さく見える。
Copyright Akiyoshi Kitaoka 2009 (June 17, 18)
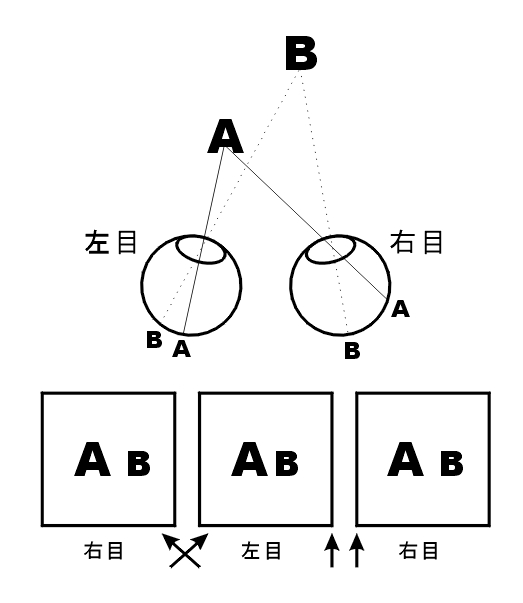
「両眼立体視の説明用の図」
図のような奥行きの位置に物体Aと物体Bがあると、右目に映るAB間の距離は、左目のそれよりも長くなる(両眼視差)。この情報を手がかりにして計算されて作られた知覚が、両眼立体視である。
Copyright Akiyoshi.Kitaoka 2006 (June 30)
---メモ---
●3枚並べるステレオグラムを考案したのは出澤正徳先生と思われるのであるが(オートステレオグラムを考案したのがタイラー先生であるのと同様)、何か証拠らしいものがないか求めたところとりあえずギブアップされたようなので(下記、2010年4月12日の電子メール)、ここではメモに留めて、機会を見つけて調査したい。こういうのはメモしておかないと後世の人にはわからなくなります。
(北岡) <2010年4月14日>
以下、出澤先生からの電子メールの一部
PS
ところで、先日の、3枚並べるステレオグラムの件ですが、小生が
印刷物として公開したのはJJAPが最初でそれ以前にはありませんでした。
最初に作ったのは1970年代半ば頃だったように思いますが、印刷物に
したことは全く覚えがありません。
そのころには、Computer Graphics の研究で、ステレオ表示した空間内に
3次元図形を直接に描くおもちゃのような道具を作って遊んでいました。
結晶物理の研究者が興味を持ち、結晶のモデルをステレオ表示する
ためにその道具を使ってくれました。当時、結晶の3次元構造を
ステレオグラムとして論文に掲載することも行われていたようなので、
3枚組のステレオグラムは、意外と結晶物理の研究者によって考えられ
既に使用されていた可能性もあると思われます。
いずれにせよ、下條さん達よりも前に使用していたとしても小生が
最初であったと主張できる証拠はありませんので、視覚研究者の
中で、最初に論文に掲載したのは、下條さん達ということで
よいと考えます。
●上記のように書いておきたいと出澤先生に連絡したところ頂いた2010年4月15日の電子メールの一部が下記です。
−−−−
3枚並べるステレオグラムを考案したのは出澤正徳先生と思われるのであるが(オートステレオグラムを考案したのがタイラー先生であるのと同様)、何か証拠らしいものがないか求めたところとりあえずギブアップされたようなので(下記、2010年4月12日の電子メール)、ここではメモに留めて、機会を見つけて調査したい。こういうのはメモしておかないと後世の人にはわからなくなります。(北岡) <2010年4月14日>
−−−−
のように書いていただいたのは、光栄なことであり、たいへんありがたいのですが、
よく考えてみると、1970年代半ば以前に誰か、たとえば、結晶物理学者など
によって、考案され、印刷物として出版されていいたか否かは不明ですが
いろいろな場面で使用されていたのではないかとの感が強くなりました。
たとえば、前のメールでの結晶物理の研究者の一人は、X線結晶解析の
桜井敏雄博士(故人)です。理研において結晶物理研究室副主任研究員、
電子計算機室長、基盤技術部長等を歴任されました。
桜井敏雄博士には、小生が理研に入所した時から公私にわたりたいへん
お世話になりました。入所後、2年目ころに、製作した「ステレオ表示した空間内に
3次元図形を直接に描く道具(ステレオ表示入力装置)」についても、いろいろと
ご協力いただきました。桜井さんの紹介でタンパク質など高分子のモデルに
取り組んでいた研究者がモデルデータのチェックや見学者等へのデモなどに
よく使用してくれました。
当時、ハードコピー装置はXYプロッタのみであり、左右の眼に対応した透視図を出力し、
それらをステレオグラムとしていました。また、当時のステレオグラムは左眼用の図を
左に右眼用の図を右に示すことが多かったので、交差融合しかできない人はうまく
観察できませんでした。そこで、平行法用のステレオグラムを横に並べて観察することに
なり、それらをのり付けし、一番右の図を切り取った3枚組のステレオグラムとして
観察しました。これは、桜井敏雄博士を含めた結晶物理関連研究者との交流の中で、
あまり意識せず、自然にそのようになったのだと思われます。
「ステレオ表示入力装置」は、現在のVRに相当するもので「VR空間内に絵を描く装置」で
あったのですが、当時、計算機の能力不足で、当初にもくろんでいた設計等の分野への
応用は実現できませんでした。その後、小生は、別の研究に取り組み、理研で脳研究が
はじまった、1988年頃になって、再び、以前とは別の観点から視覚の研究に取り組み出し、
平行法のステレオグラムのみでは観察できない人が多いので、10年以上前を
思い出し、論文では3枚組のステレオグラムを使用するようにしているというわけです。
以上、思い起こしてみると、結晶物理関連研究者、特に、桜井敏雄博士などは
3枚組のステレオグラムにすれば多くの人に対応できるようになることを既に
知っておられたのではないかと推察されます。すなわち、最初に
考案したのは小生ではないということになります。
それでは
●ますます自覚的に3枚組みを使い始めたのは出澤先生ではないかとの感を強めました。 (北岡) <2010年4月15日>