第4回錯覚ワークショップ 明治大学駿河台キャンパス アカデミーコモン9階 講義室309A
3月13日(火) 15:30 – 16:20 プログラム
計算可能な錯視の探索的検討
北岡 明佳 (立命館大学 文学部 心理学専攻 /JST,CREST) email HP
since March 6, 2012 抄録
<本日の話題>
1. 渦巻き錯視の数理
2. 線遠近法の数理とリーマン空間?
3. 視覚的補完(主観的輪郭)とベジェ曲線
4. フレーザー・ウィルコックス錯視群
5. 傾き錯視と同居する静止画が動いて見える錯視群
1. 渦巻き錯視の数理
同心円(中心が同じ複数の円)が渦巻きに見える現象

「カフェウォール渦巻き 2011年リメーク版」
灰色の同心円が左に回転して中心に向かう渦巻きに見える。
Copyright Akiyoshi Kitaoka 2011 (March 1)

カフェウォール錯視
灰色の水平線が左に傾いて見える。

"Spiral warp"
Concentric rings appear to be spirals.
Copyright Akiyoshi Kitaoka 2007 (June 29)
equiangle = 45 deg
The spiral illusion of the Zöllner illusion:
Kitaoka, A., Pinna, B., and Brelstaff, G. (2001). New variations of spiral illusions. Perception, 30, 637-646.

ツェルナー錯視
水平線が上から交互に右・左・右・左に傾いて見える。

"Cyanophyceae spiral"
Concentric circles appear to be a spiral.
Copyright Akiyoshi Kitaoka 2007 (August 29)

First presented by Fraser (1908); Reproduced by Akiyoshi Kitaoka (2009)
Fraser's spiral
The term "spiral illusion" had long referred to the spiral illusion of the Fraser illusion (Fraser, 1908) before we elucidated that any tilt illusion can form spiral illusion (Kitaoka, Pinna and Brelstaff, 2001). This page shows a copy of Fraser's spiral produced by PC programming. <2003/8/30>
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
北岡明佳 (2006) 渦巻き錯視のメカニズム じっきょう数学資料, 52, 13-15. PDF

"Fractal spiral illusion"
Concentric rings made up of fractal islands appear to form spirals.
Copyright Hitoshi & Shinobu Arai
2007
from Professor Hitoshi Arai,
Graduate School of Mathematical Sciences, University of Tokyo, October 4,
2007
北岡明佳のコメント: 原理としてはフレーザー錯視のようですが、それよりもなによりも、世界初のフラクタル錯視図形 なのではないでしょうか!? 新井先生の視覚数学e研究室報告に、この錯視の論文が出ました。 <2007年10月4日>
Suggested function
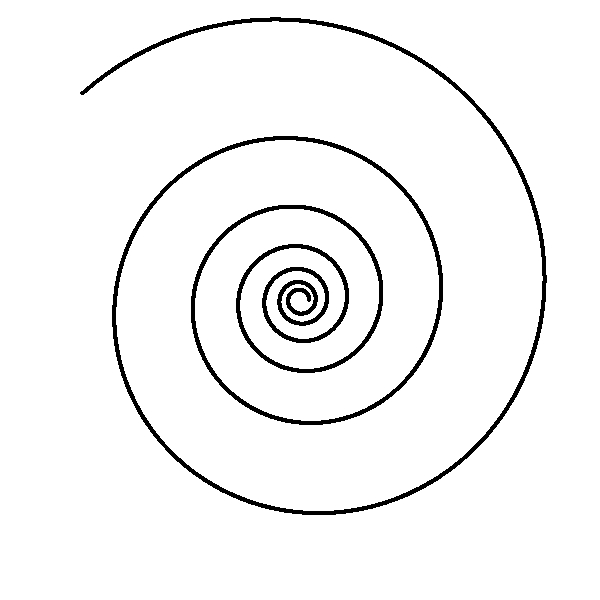
Bernoulli's spiral
r = a exp (k θ)
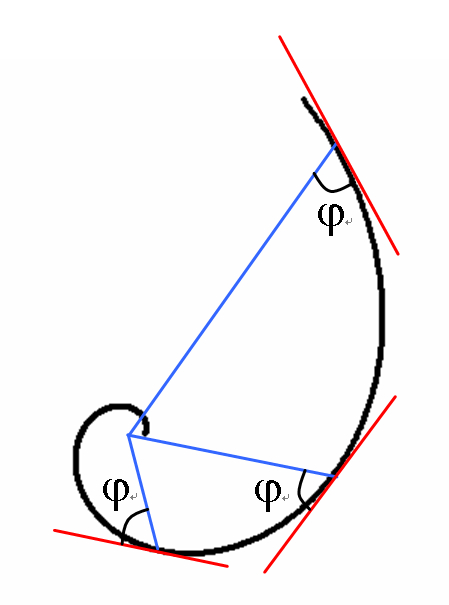
= equiangular spiral
k = 1 / tan (φ)

Spiral Glass pattern
φ = 70º
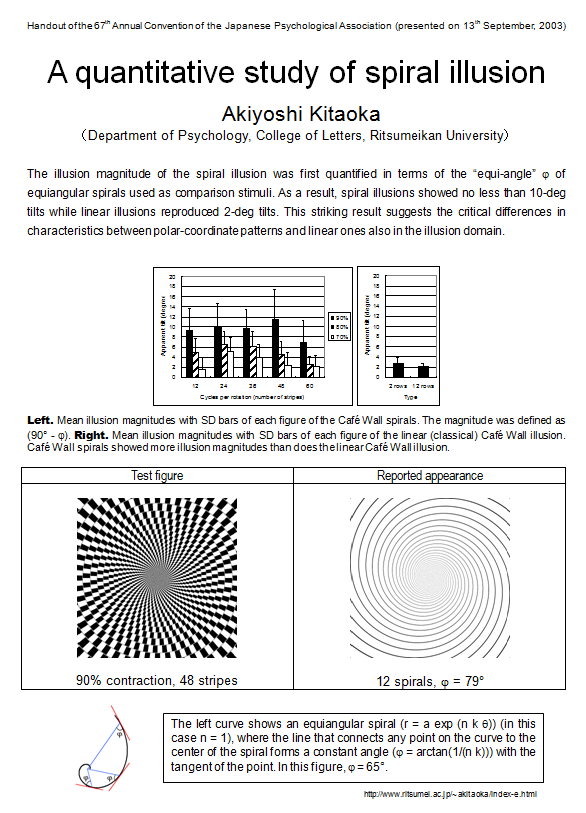
結論 渦巻き錯視はベルヌーイ螺旋の知覚メカニズムで説明できる。
 Kitaoka, A., Pinna, B., and Brelstaff, G. (2001). New variations of spiral illusions. Perception, 30, 637-646. PDF
Kitaoka, A., Pinna, B., and Brelstaff, G. (2001). New variations of spiral illusions. Perception, 30, 637-646. PDF
2. 線遠近法の数理とリーマン空間?
網膜座標系と錯視
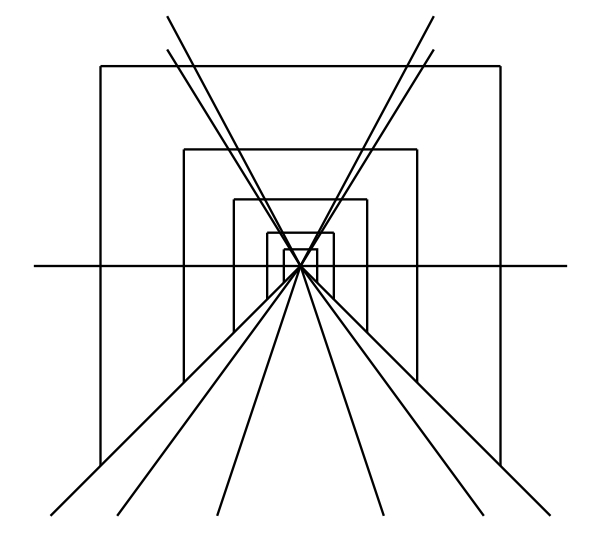
問: 網膜地図(retinal map)は、中心を決め、中心を通る上下・左右の軸を決めると、中心からの距離(視角)で座標を表す。理想的な視野世界はどのように網膜地図に投射されるか?
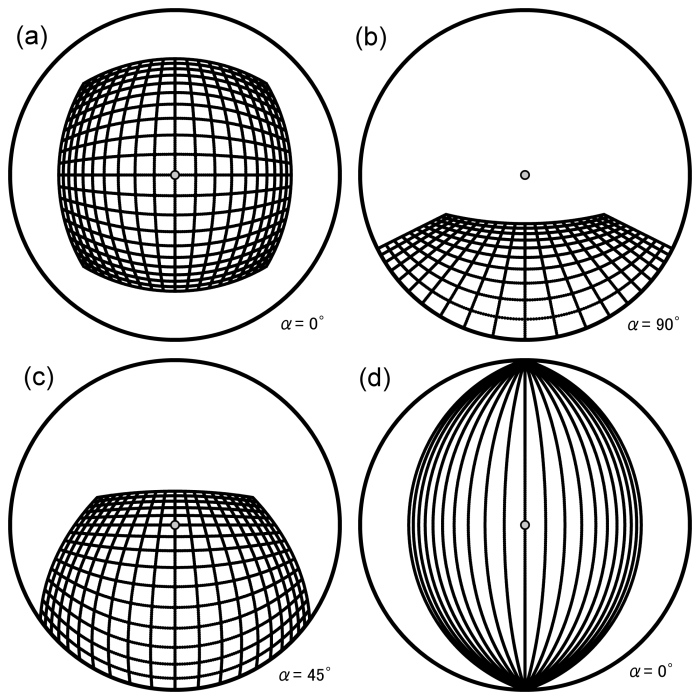
Figure 1. An instance of retinal coordinates. Suppose that twenty by twenty squares (each being 10 cm x 10 cm) are drawn at the center of an infinitely-extended flat plane and observed from 50 cm apart. (a) When the plane is perpendicular to the visual axis, the mesh appears to bulge out though it really has no curves. (b) When the visual axis is parallel to the plane, the lines parallel to the visual axis appear to converge at the center of the visual field while the lines perpendicular to the visual axis (except those that cross the visual axis) appear to curve outward. (c) When the plane is observed obliquely, both (bulging and converging) appearances coexist. (d) Parallel lines on a plane perpendicular to the visual axis meet at two points on the surrounding circle. The gray circle at the center in each panel represents the foveal vision. The radius of the circle is 90 degree of visual angle.
Given equations

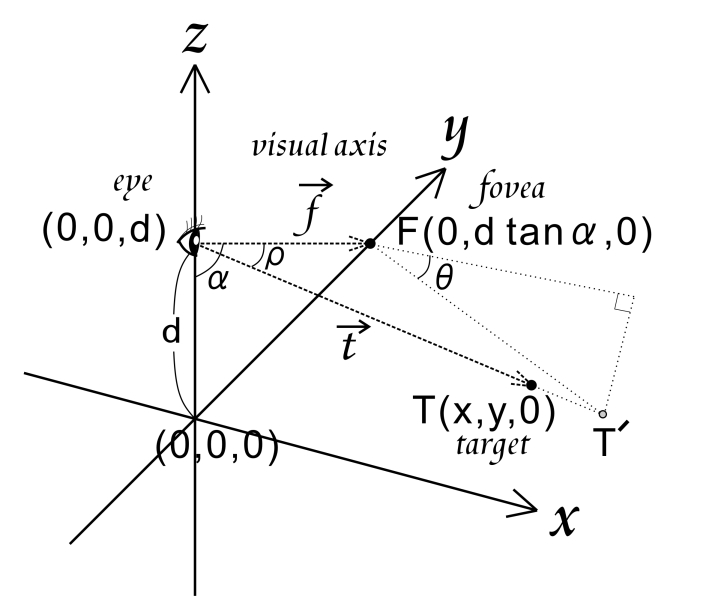
Figure Appendix. The method to obtain the retinal coordinates (ρ,θ) from the visual world. Suppose that the seen object is placed on the x-y plane where a target point T (x, y, 0) is located, and that an observing eye is located on the z-axis with the height of "d". "α" is the angle between the visual axis and the z-axis when the eye sees a point F (foveal point) that is located on the y-axis. The visual angle "ρ" of the target point is the angle between the line from the eye to the foveal point F (vector f) and the line from the eye to the target point T (vector t). The visual angle ρ is obtained from these two vectors. The angle θ is given as the angle between the line parallel to the x-axis through the foveal point F and the line from the foveal point F to another point T´ where the extension of vector t meets the plane that is perpendicular to the visual axis (or vector f) and passes through the foveal point F.
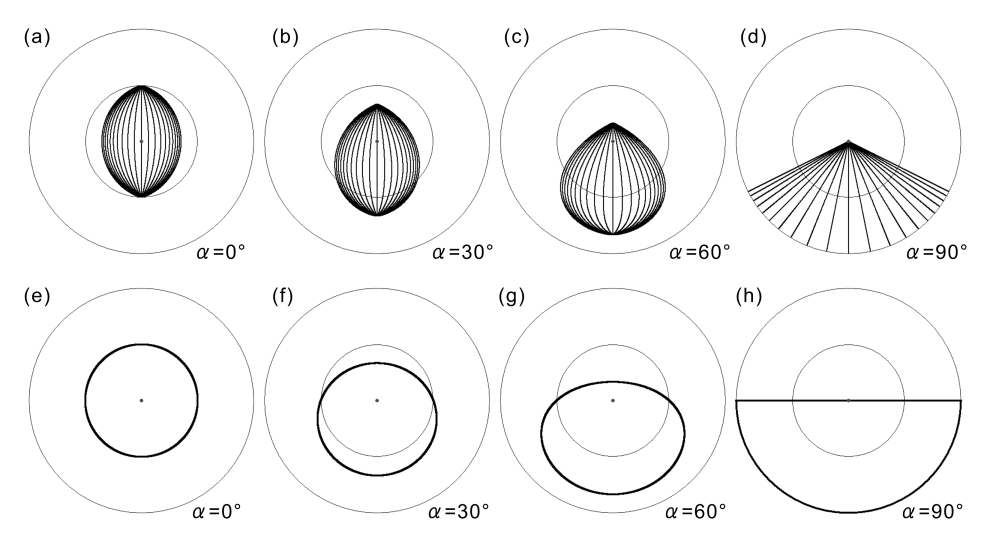
Figure 2. Extended retinal coordinates. The radius of the outer circle represents 180 degrees of “visual angle” while the radius of the inner one shows 90 degrees of visual angle. (a) The image of Figure 1d is placed in these coordinates. (b) and (c) The same image is seen obliquely. (d) The same image is seen in parallel to the plane. (e)-(h) The thick line shows the line at infinity of a plane within which the entire plane is represented.
結論 網膜座標地図は無限を表現することができる。
 Kitaoka, A. (2007) Psychological approaches to art. Japanese Journal of Psychonomic Science,26, 97-102. PDF
Kitaoka, A. (2007) Psychological approaches to art. Japanese Journal of Psychonomic Science,26, 97-102. PDF
3. 視覚的補完(主観的輪郭)とベジェ曲線
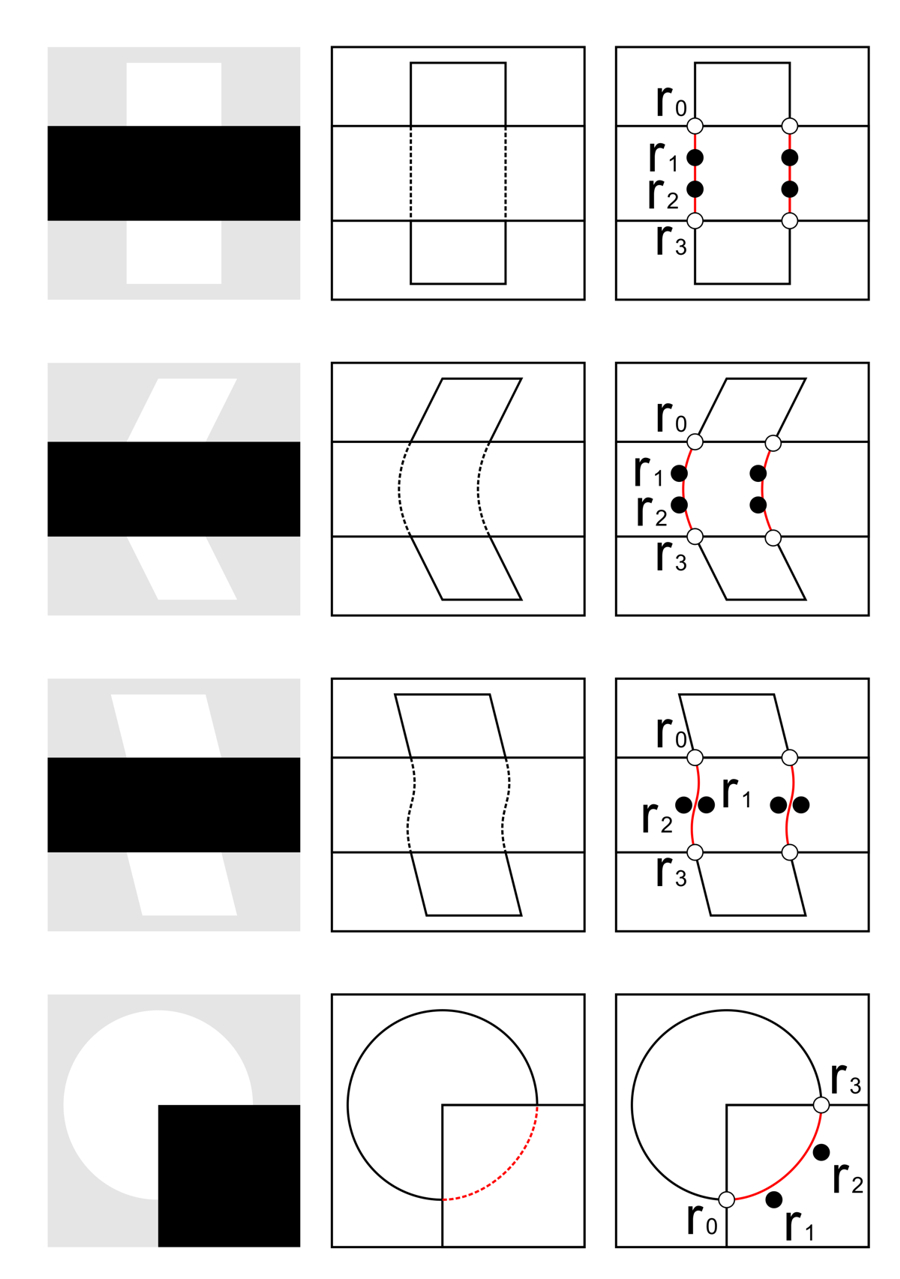
結論 視覚的補完の形状はベジェ曲線(4つのコントロールポイントを持つ3次曲線)で近似できる。
 論文出していないので、誰も知らない。
論文出していないので、誰も知らない。
Kitaoka, A., Sakurai, K., Gyoba, J., and Kawabata, H. (頓挫中) Visually interpolated contours can be described by cubic Bézier curves.
4. フレーザー・ウィルコックス錯視群

「蛇の回転」
蛇の円盤が勝手に回転して見える。
Copyright A.Kitaoka 2003 (September 2, 2003)
(配布物)
「最適化型」フレーザー・ウィルコックス錯視・タイプ I
Optimized Fraser-Wilcox illusion, Type I

「赤い蛇の回転の詰め合わせ」
リングがゆっくり、あるいは急速に回転して見える。
Copyright Akiyoshi Kitaoka 2008 (March 19)
「最適化型」フレーザー・ウィルコックス錯視・タイプ IIa
Optimized Fraser-Wilcox illusion, Type IIa

「最適化型」フレーザー・ウィルコックス錯視・タイプ III
Optimized Fraser-Wilcox illusion, Type III

「影付きの左右に動く蛇」
蛇が左右に動いて見える。
Copyright Akiyoshi Kitaoka 2009 (June 7)
「最適化型」フレーザー・ウィルコックス錯視・タイプ IV
Optimized Fraser-Wilcox illusion, Type IV

「錠剤の回転」
(たくさん版)
錠剤のリングが回転して見える。
Copyright Akiyoshi Kitaoka 2009 (March 24)
赤と紫特有の「最適化型」フレーザー・ウィルコックス錯視・タイプ V
Optimized Fraser-Wilcox illusion, Type V

「オニシバリの実の回転」
オニシバリの実のリングが回転して見える。
Copyright Akiyoshi Kitaoka 2008 (December 19)
最適化型フレーザー・ウィルコックス錯視・タイプVの作品いろいろ
最適化型フレーザー・ウイルコックス錯視群
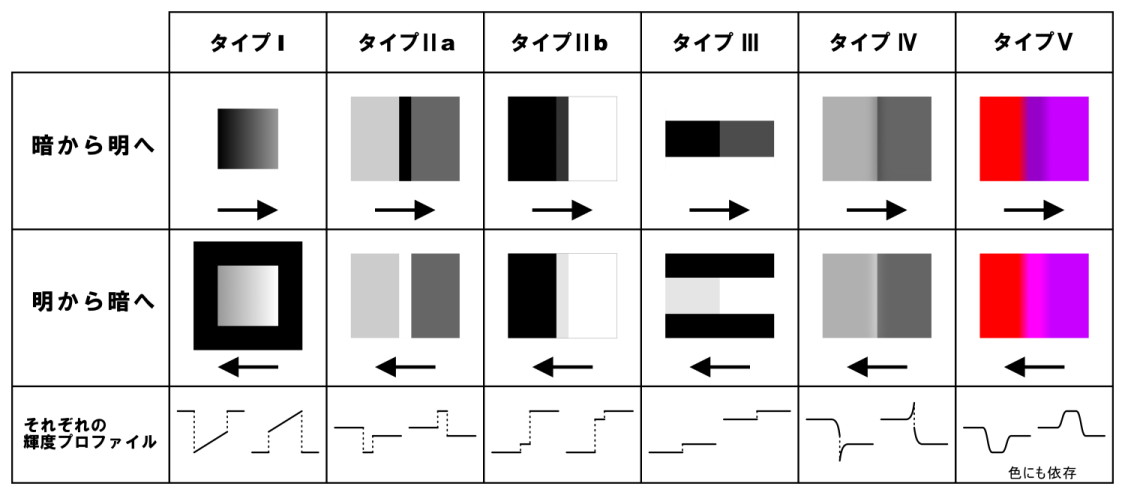
Kitaoka, A. (2007) Phenomenal classification
of the “optimized” Fraser-Wilcox illusion and the effect of color. Poster
presentation in DemoNight, VSS2007, GWiz, Sarasota, Florida, USA, May 14,
2007.
Kitaoka, A. (2008) Optimized Fraser-Wilcox illusions: A pictorial classification by Akiyoshi Kitaoka. Talk in a workshop (WS005) in the 72nd Annual Convention of the Japanese Psychological Association, Hokkaido University, Sapporo, September 19, 2008. Presentation page
北岡明佳 (2008) 人はなぜ錯視にだまされるのか? トリック・アイズ メカニズム カンゼン
これらは、 黒→濃い灰色→白→薄い灰色→黒 の方向に動いて見える錯視群である。
Direction: black → dark-gray → white → light-gray → black
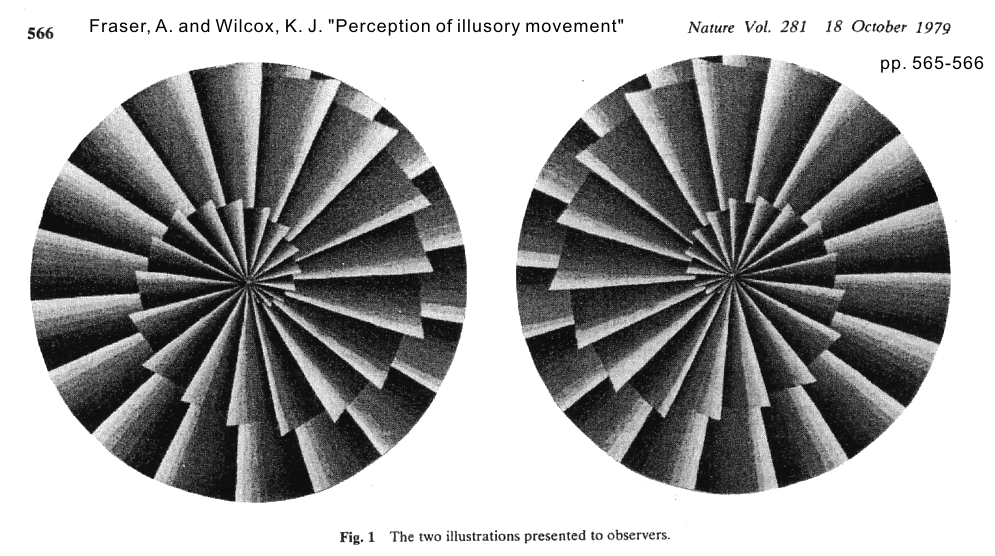
Fraser, A. and Wilcox, K. J. (1979) Perception of illusory movement. Nature, 281, 565-566.
perceptual dimorphism とその遺伝性を主張した。
Alex Fraser - Gallery of Paintings
2. Faubert and Herbert (1999)
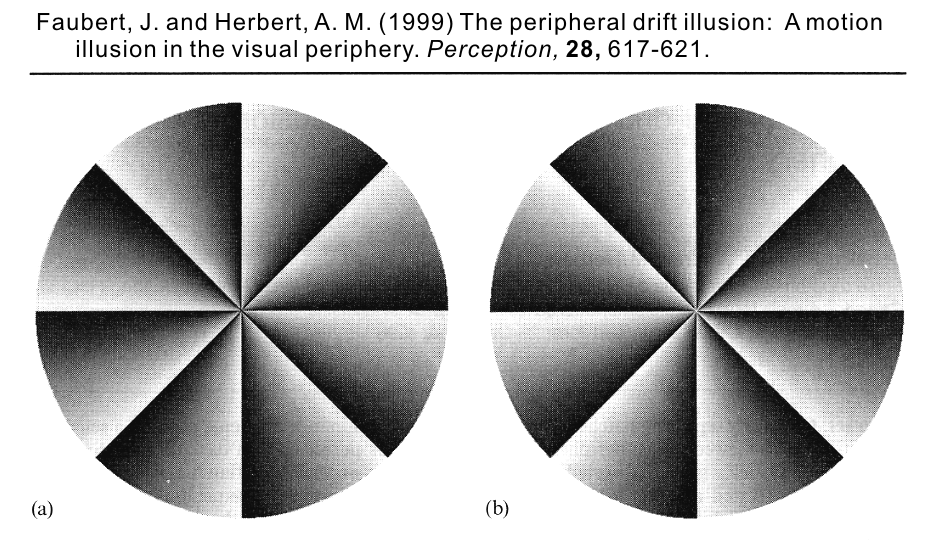
Faubert, J. and Herbert, A. M. (1999) The peripheral drift illusion: A motion illusion in the visual periphery. Perception, 28, 617-621.
3. Naor-Raz and Sekuler (2000)
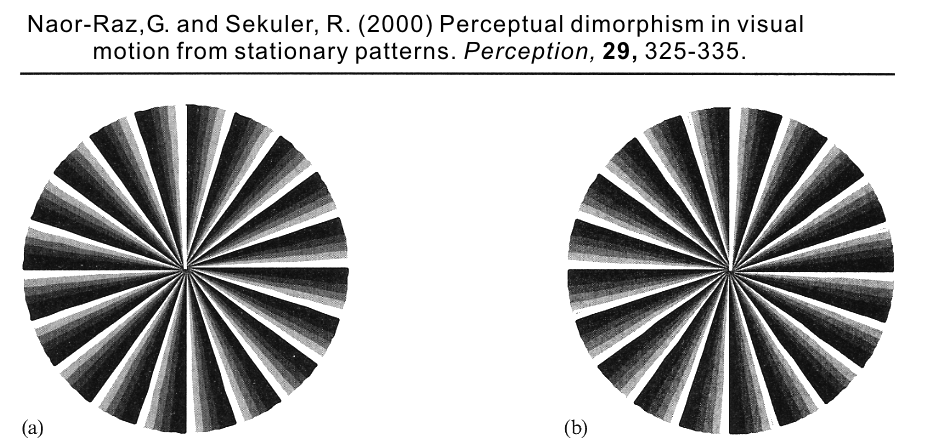
Naor-Raz, G. and Sekuler, R. (2000) Perceptual dimorphism in visual motion from stationary patterns. Perception, 29, 325-335.

Kitaoka, A. and Ashida, H. (2003) Phenomenal characteristics of the peripheral drift illusion. VISION (Journal of the Vision Society of Japan), 15, 261-262

"Dark to light" (in gradation) might be stronger.

"Light to dark" might be stronger.

"Dark to light"

"Light to dark"

"Dark to light" and "light to dark" in cooperation
 I propose an empirical observation that color might enhance the illusion
in some conditions.
I propose an empirical observation that color might enhance the illusion
in some conditions.

Observation 1. The illusion from dark to light is enhanced by red or blue.

Observation 2. The illusion from light to dark is enhanced by yellow or green.

Observation 3. The illusion from dark to light is enhanced by red or blue, while the illusion from light to dark is enhanced by yellow or green. Both illusions work additively.
 最近の発見で、またややこしいことに・・・
最近の発見で、またややこしいことに・・・フレーザー・ウィルコックス錯視図の一種(背景は灰色)

Darkening disambiguation


赤いと反対方向

グラデーションは関係なし?


赤い perceptual dimorphism


赤い perceptual dimorphism もグラデーションは不要?


「フレーザー・ウィルコックス錯視族のレビュー」論文
Kitaoka, A. (2012?) The Fraser-Wilcox illusion and its extension. Shapiro, A. and Todorovic, D. (Eds.), Oxford Compendium of Visual Illusions. Oxford University Press.
を乞うご期待
5. 傾き錯視と同居する静止画が動いて見える錯視群
Tilt illusion is a subcategory of geometrical illusion, in which lines or edges appear to tilt clockwise or counterclockwise. (e.g., Zöllner illusion, Fraser illusion, Café Wall illusion)
Anomalous motion illusion refers to motion illusion in a stationary image, in which part of the
stationary image appears to move. (e.g., Ouchi illusion, Enigma illusion,
optimized Fraser-Wilcox illusion)
Some* types of tilt illusions are accompanied by anomalous motion illusion. (e.g., Illusion of Y-junctions)
*Later, I have realized that most of tilt illusions (including the Fraser illusion and the Café Wall illusion) share the same image with anomalous motion illusion.

"The autumn color swamp"
The inset appears to move.
Copyright A.Kitaoka 2000, 2003, 2007, 2010
<Handout>

The two concentric arrays of stars appear to rotate in the different directions when we approach or move away from the figure while fixating at the center.
Copyright Akiyoshi Kitaoka 2000, 2010
<Handout>
Illusion of Y-junctions
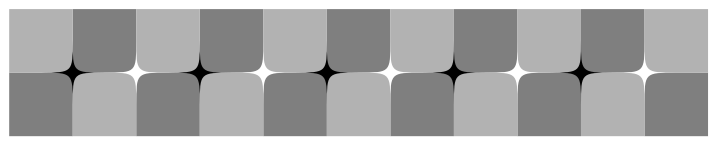
The elemental image as the tilt illusion
The horizontal edge on which black or white stars are placed appears to tilt counterclockwise.
Kitaoka, A., Pinna, B., and Brelstaff, G. (2001). New variations of spiral
illusions. Perception, 30, 637-646.
Kitaoka, A., Pinna, B., and Brelstaff, G. (2004). Contrast polarities determine the direction of Cafe Wall tilts. Perception, 33, 11-20.

The elemental image as anomalous motion illusion
The inset appears to move. When the retinal image is moved vertically, the inset appears to move horizontally. When the retinal image is moved horizontally, the inset appears to move vertically.
<Handout>
Today's talk
1. "Discovery" of the Fraser illusion family
2. Anomalous motion illusion accompanied by tilt illusion
3. A speculation of the "Rotating snakes" illusion
§1. "Discovery" of the Fraser illusion family

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.

Fraser's spiral
(spiral illusion of the Fraser illusion)
Concentric circles of "twisted cords" appear to be spirals.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
<Handout>

In December 2009, I developed a "new" illusion (though it essentially was not new), which I called the "pseudo Fraser illusion".

"Pseudo Fraser
spirals"
Concentric rings appear to be spirals.
Copyright Akiyoshi Kitaoka 2009 (December 17)

Psudo-Fraser illusion
("Fraser's Café Wall" illusion)
The middle lines are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)

Pseudo-Fraser's spiral
(spiral illusion of the "Fraser Café Wall" illusion)
Concentric circles of "twisted cords" appear to be spirals.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Q. What are the differences between the Fraser illusion and the pseudo-Fraser illusion?
A. There are three factors involved:
1. whether the inducers are obliques (Fraser illusion) or not (pseudo-Fraser illusion)
2. whether the inducers are only lines (Fraser illusion) or combination of lines and edges (pseudo-Fraser illusion)
3. whether the inducers are two (Fraser illusion) or four (pseudo-Fraser illusion)
1. whether the inducers are obliques (Fraser illusion) or not (pseudo-Fraser illusion)
Finding: There are counterparts of the Fraser illusion as well as the pseudo-Fraser illusion, respectively

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
The counterpart of the Fraser illusion

Illusion of shifted lines
Rows of middle line segments are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Kitaoka, A. (2007) Tilt illusions after Oyama (1960): A review. Japanese Psychological Research, 49, 7-19.

Psudo-Fraser illusion
("Fraser's Café Wall" illusion)
The middle lines are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
The counterpart of the pseudo-Fraser illusion

The patterns like "twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
2. whether the inducers are only lines (Fraser illusion) or combination of lines and edges (pseudo-Fraser illusion)
Finding: There are three groups in this sense, only lines, combinations of lines and edges, and only edges, respectively
Lines only

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
Combination of lines and edges

"Cafe Wall Fraser" illusion
The patterns like "twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
Edges only

Illusion of oblique edges
Rows of oblique edges are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Kitaoka, A. (2007) Tilt illusions after Oyama (1960): A review. Japanese Psychological Research, 49, 7-19.
3. whether the inducers are two (Fraser illusion) or four (pseudo-Fraser illusion)
Finding: The basic components of the Fraser illusion can be counted four to match the pseudo-Fraser illusion. In the same way, The basic components of the pseudo-Fraser illusion can be counted two to match the Fraser illusion. Thus, this factor is not essential for tilt illusion.

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
The counterpart of the Fraser illusion

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.

Psudo-Fraser illusion
("Fraser's Café Wall" illusion)
The middle lines are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
The counterpart of the pseudo-Fraser illusion

Psudo-Fraser illusion
("Fraser's Café Wall" illusion)
The middle lines are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
cf. Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
Conclusion: The Fraser illusion family consists of six (3 x 2) illusions.
<Handout>
Q. How is the pseudo-Fraser illusion related to the Café Wall illusion?
A. I think they are essentally the same illusion.


The pseudo-Fraser illusion (left) and the Café Wall illusion (right)

Café Wall illusion: a standard image
cf. Gregory, R. L. and Heard, P. (1979) Border locking and the Café Wall illusion. Perception, 8, 365-380.
Q. Does tilt illusion occur where contast polarity changes?
A. Yes, as if it were the reversed phi (the direction opposite to the shift).
(Illusion of oblique edges)
(Illusion of shifted lines)
Example

"Derby man tilt illusion"
Horizontally aligned rows of "derby men" appear to tilt alternately. From the top, counterclockwise, clockwise, and so on.
Copyright Akiyoshi Kitaoka 2010 (March 21)
My idea: There are eight fundamental combinations of basic components.
(I imagine that neurons with receptive fields like these play a part)
(The limiting case of the Fraser illusion family)
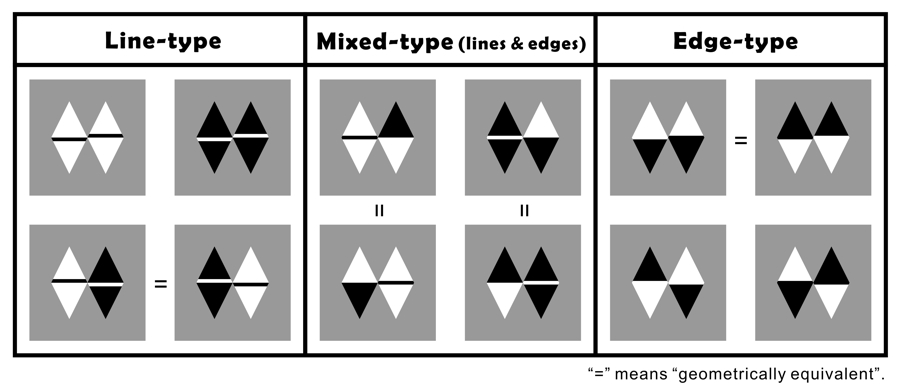
In each gray square, the middle line or edge appears to tilt counterclockwise.
Copyright Akiyoshi Kitaoka 2010 (March 22)
In addition: Café Wall illusion can be explained with this idea.

Café Wall illusion: a standard image
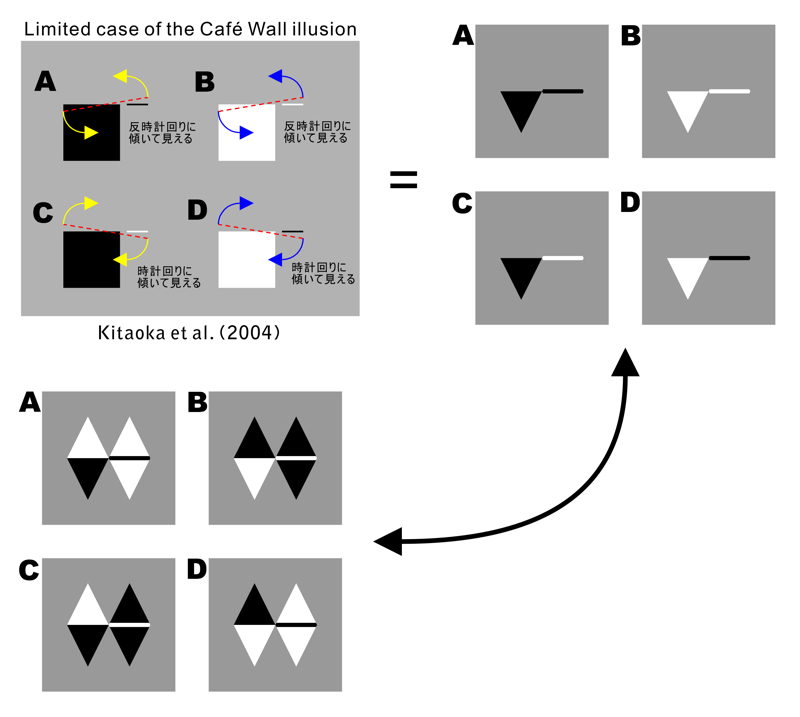
Copyright Akiyoshi Kitaoka 2010 (March 22)
Kitaoka, A., Pinna, B., and Brelstaff, G. (2004) Contrast polarities determine the direction of Café Wall tilts. Perception, 33, 11-20.
§2. Anomalous motion illusion accompanied by tilt illusion

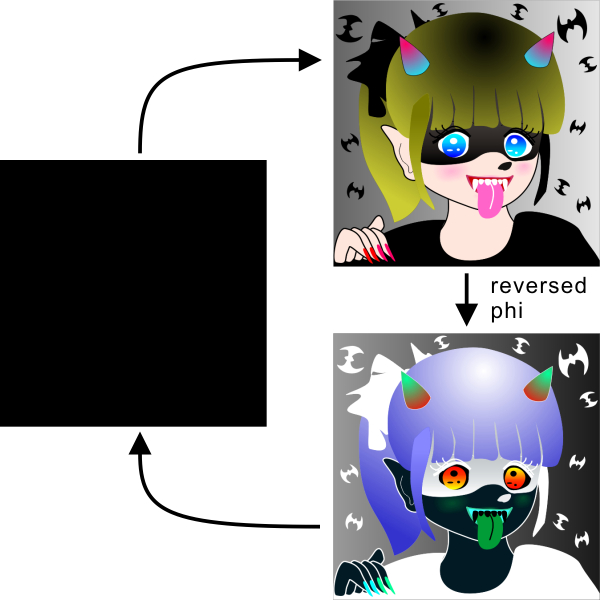
"Obake-hime"
obake = ghost; hime = princess or girl
The face appears to expand; the group of bats appears to rotate counterclockwise. This is Professor Mather's four-stroke motion.
Copyright Akiyoshi Kitaoka 2009 (August 10)
Professor Mather's demonstration is the best.
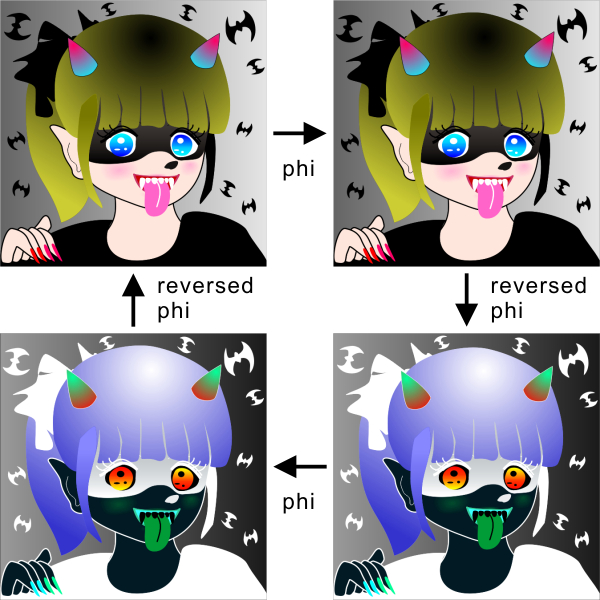
Copyright Akiyoshi Kitaoka 2010 (March 22)
(Reversed phi only)

Copyright Akiyoshi Kitaoka 2010 (March 22)
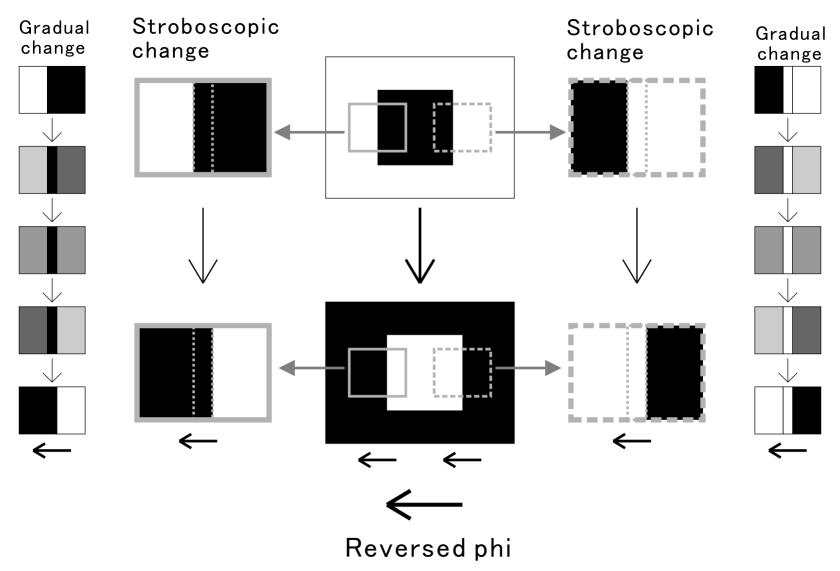
Reversed phi movement (Anstis and Rogers 1975). There are four rectangles, each of which is flanked by thin lines that are dark or light. When the luminance of the rectangles decreases and that of the background increases accordingly, the upper two appear to converge in motion while the lower two appear to go apart in motion. On the other hand, when the luminance of the rectangles increases and that of the background decreases accordingly, the upper two appear to go apart in motion while the lower two appear to approach each other in motion. In sum, the direction of apparent motion is from the dark flank to the neighboring part that goes darkening or from the light flank to the neighboring part that goes brightening. Although the rectangles are aligned vertically, the apparent positional displacement occurs in the opposite direction to motion. If observers cross-fuse (uncross-fuse) the right and left rectangles, the upper rectangle appears to be in front of (behind) the lower one when they are dark.
Kitaoka, A. (2006) Configurational coincidence
among six phenomena: A comment on van Lier and Csathó (2006). Perception,
35, 799-806. animations ![]()
Anstis S M, 1970 “Phi movement as a subtraction process” Vision Research 10 1411-1430
Anstis S M, Rogers B J, 1975 “Illusory reversal of visual depth and movement during changes of contrast” Vision Research 15 957-961
4-stroke motion corresponding to the Line Type

Copyright Akiyoshi Kitaoka 2010 (March 22)

Finding: The direction of motion is the same as the tilt illusion.
Mather, G. and Murdoch, L. (1999) Second-order processing of four-stroke apparent motion. Vision Research, 39, 1795-1802.
cf. van Lier R, Csathó Á, 2005 “Dancing shapes: A comparison of luminance induced distortions” Perception, 35, 775 – 798.
4-stroke motion corresponding to the Edge Type

Copyright Akiyoshi Kitaoka 2010 (March 22)

Finding: The direction of motion is the same as the tilt illusion.
cf. van Lier R, Csathó Á, 2005 “Dancing shapes: A comparison of luminance induced distortions” Perception, 35, 775 – 798.
4-stroke motion corresponding to the Mixed Type

Copyright Akiyoshi Kitaoka 2010 (March 22)

Finding: The direction of motion is the same as the tilt illusion.
<Takeuchi's four-stroke motion>
Takeuchi, T. (1997) The motion analogue of the cafe wall illusion. Perception, 26, 569-584.
Then, anomalous motion illusions that coexist in tilt illusion images can be explained in this context.
When the retinal image slides in the special direction, the orientation along which the tilt illusion occurs, the four-stroke motion is induced and anomalous motion illusion is observed.
Copyright Akiyoshi Kitaoka 2010 (June 26)
<Handout>

"Rain"
The inset appears to move.
Copyright Aliyoshi Kitaoka 2005 (July 2)
Explanation of the illusion of Y-junctions

Drawn by Aliyoshi Kitaoka 2010 (June 25)

(Takeuchi's four-stroke motion)
<Two dimensional displays>

Illusion of Y-junctions
Kitaoka, A., Pinna, B., and Brelstaff, G. (2001). New variations of spiral
illusions. Perception, 30, 637-646.
Kitaoka, A., Pinna, B., and Brelstaff, G. (2004). Contrast polarities determine the direction of Cafe Wall tilts. Perception, 33, 11-20.


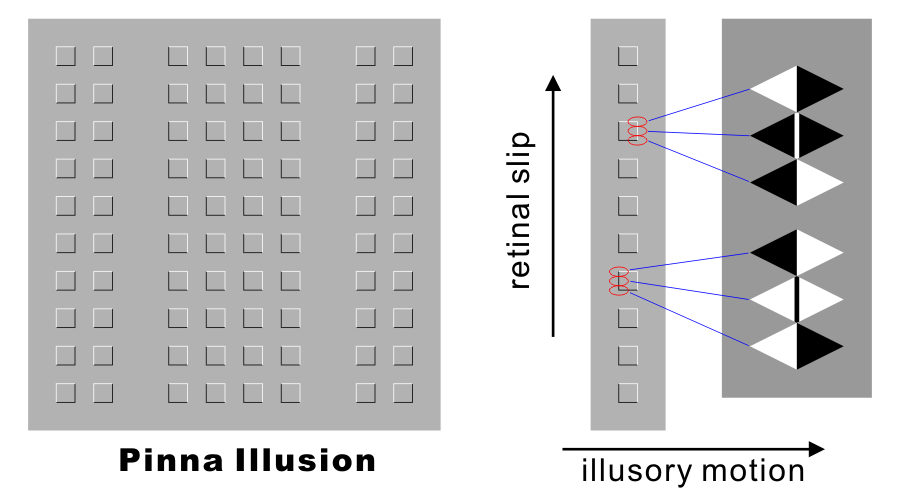
Pinna Illusion
Pinna, B. and Brelstaff, G. J. (2000) A new visual illusion of relative motion. Vision Research, 40, 2091-2096.
Explanation of the Pinna illusion
New: This idea led me to produce a novel illusion "spine drift illusion".
"Spine drift
illusion"
The inset appears to move.
Copyright Akiyoshi Kitaoka 2010 (June 4)

"Spine drift illusion"
The inset appears to move.
Copyright Akiyoshi Kitaoka 2010 (July 6)

"Spine drift
illusion with the illusion of shifted lines"
The inset appears to move.
Copyright Akiyoshi Kitaoka 2010 (June 5)
"Hamburger drift
illusion"
The inset appears to move.
Copyright Akiyoshi Kitaoka 2010 (June 6)
ECVP2010(ローザンヌ)での発表
Kitaoka, A. (2010) The Fraser illusion family and the corresponding motion illusions. 33rd European Conference on Visual Perception (ECVP 2010), EPFL, Lausanne, Switzerland, 2010/8/22-26, 8/26 poster publication. Poster (Kitaoka, A. (2010) The Fraser illusion family and the corresponding motion illusions. Perception, 39, Supplement, #61, p. 178)
参考書
北岡明佳著 錯視入門 朝倉書店 (2010年7月) ![]() new!
new!
北岡明佳著 人はなぜ錯視にだまされるのか? トリック・アイズ メカニズム カンゼン (2008年7月刊行) ![]() new!
new!
北岡明佳(監修) ニュートン別冊 脳はなぜだまされるのか? 錯視
完全図解 (2007年10月刊行) ![]()
北岡明佳著 だまされる視覚 錯視の楽しみ方 化学同人 (2007年1月刊行) 好評発売中 ![]()

まとめ
錯視と数学には深い関係がある。
 ご清聴ありがとうございました。
ご清聴ありがとうございました。

3月13日(火)
10:00-10:10 あいさつ
10:10-11:00 「視覚復号型暗号 ― 画像が見える暗号」
山口泰(東京大学大学院総合文化研究科/JST,CREST)
11:10-12:00 「サグ部の自然渋滞緩和に向けて~錯視現象とその緩和策~」
友枝明保(明治大学研究・知財戦略機構/JST,CREST)
(昼休み)
13:30-14:20 「錯覚は聴覚コンテンツ・味覚コンテンツに応用できるか?」
宮下芳明(明治大学理工学部/JST, CREST)
14:30-15:20 「経済的活動に対する認知バイアスと知識の影響」
植田一博(東京大学大学院情報学環・学際情報学府/JST, CREST)
15:40-16:30 「視覚神経科学と錯視」
藤田一郎(大阪大学大学院生命機能研究科)
16:40-17:30 「錯覚科学による社会的価値創造~例、エンタテイメント分野への応用~」
川勝良昭(新潟県立大学客員教授)
18:00-20:00 懇親会(会費制,要予約)
3月14日(水)
10:00-10:50 「画像知覚のひずみと誇大広告の危険性」
杉原厚吉(明治大学大学院先端数理科学研究科/JST,CREST)
11:00-11:50 「写真空間の知覚的性質:写真はどこまで真を写しているか?」
松田隆夫(立命館大学立命館グローバルイノベーション研究機構)
(昼休み)
13:30-14:20 「数理モデリングとそのアート、ファッションへの応用」
合原一幸(東京大学生産技術研究所)
14:30-15:20 「社会的知覚における錯覚 -生き物らしさ,人らしさの知覚-」
福田玄明(東京大学大学院総合文化研究科/JST, CREST)
15:30-16:20 「計算可能な錯視の探索的検討」
北岡明佳(立命館大学文学部/JST,CREST)