Spirals 2
since March 22, 2023

Helix

Bernoulli's spiral

Archemedes's spiral
Helix
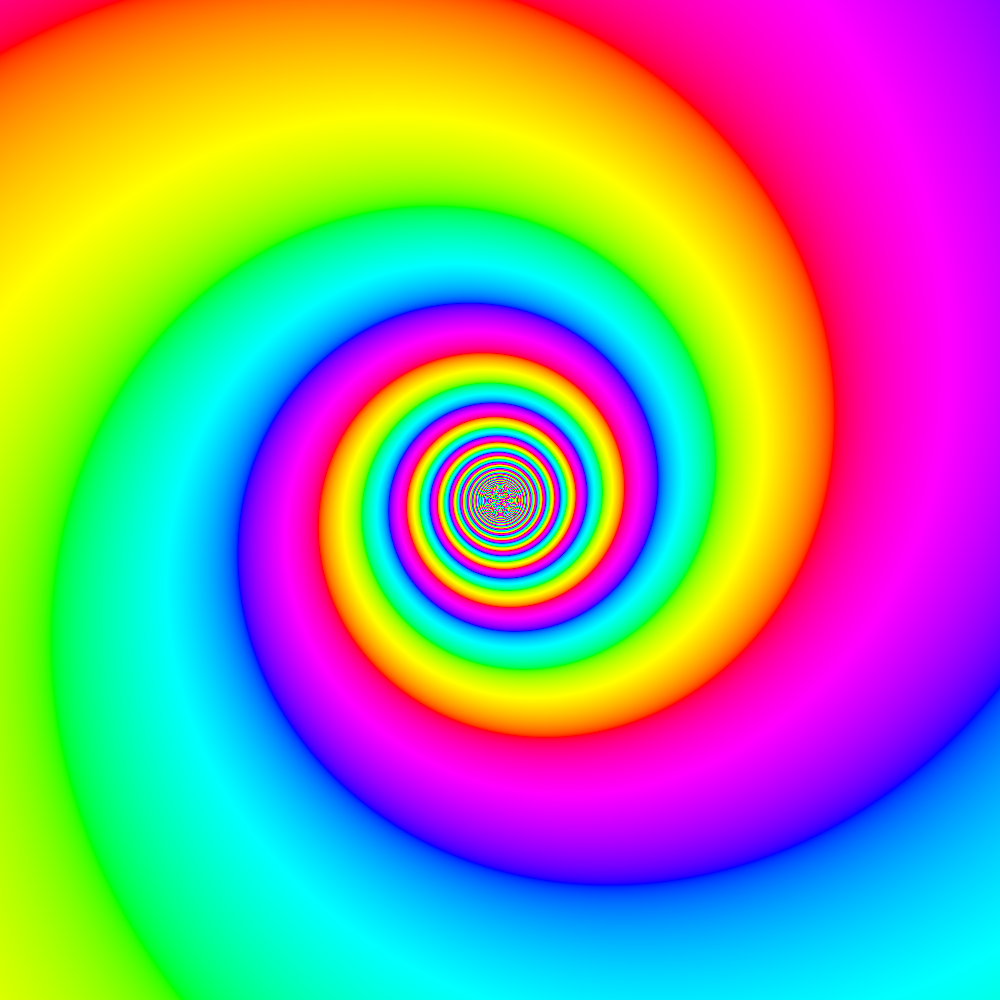
Bernoulli's spiral

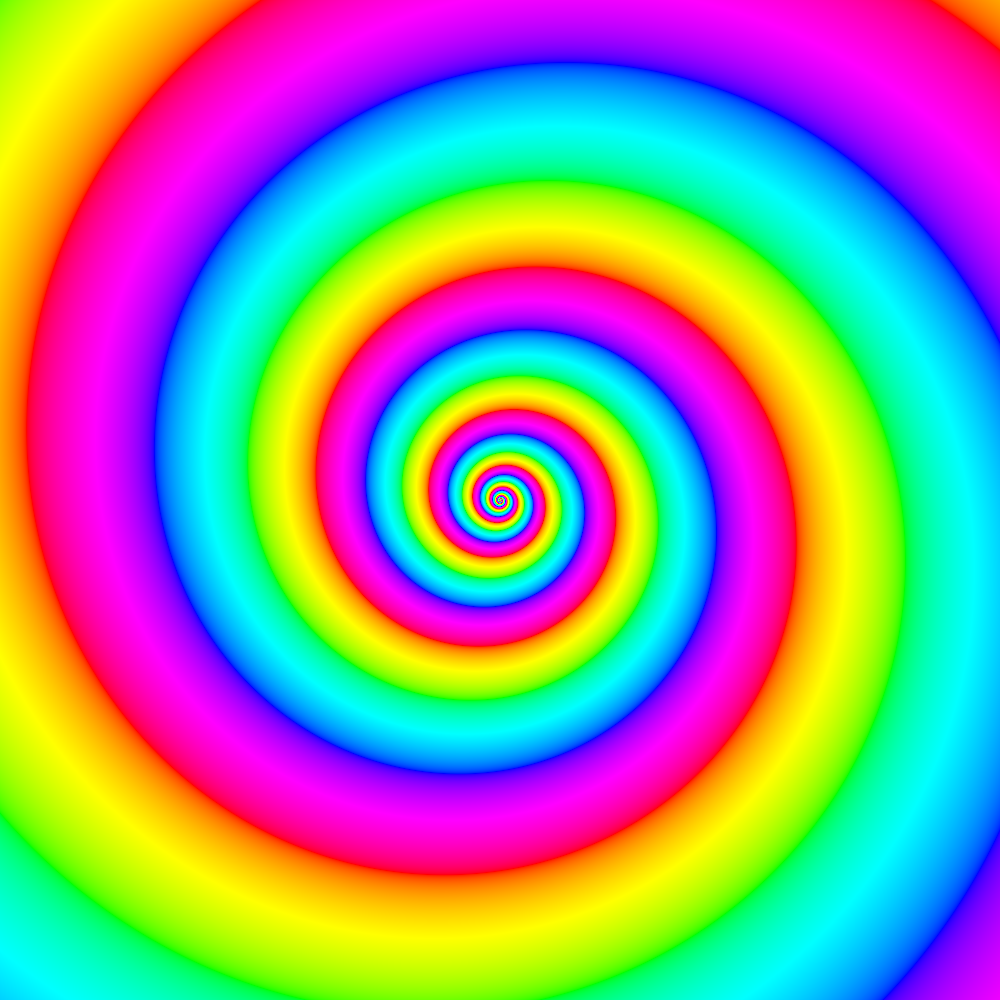
Archemedes's spiral

100 x 100 deg

10 x 10 deg

100 x 100 deg

10 x 10 deg
Tube (concentric helix)

concentric Benoulli's spiral

concentric Archemedes's spiral
Bernoulli's spiral: r = a exp (kθ) (ベルヌーイの渦巻き、ベルヌーイの螺旋、対数螺旋(logarithmic spiral)、等角螺旋(equiangular spiral)などと呼ばれる。ただし、螺旋は helix と対応する概念を表した用語と考えるのであれば誤訳であり、対数螺旋は対数的渦巻き、等角螺旋は等角的渦巻きと呼ぶべきかもしれない)
渦巻きが1本の場合: r = a exp (kθ)
渦巻きがn本の場合: r = (r1, r2, … ri, … rn)
ri = a exp (k(θ+ 2π(i - 1) / n) )
ρ: reduction ratio (縮小率), n: number of spirals (渦巻きの本数), phi (φ): angle between the line connecting the center with a particular point on a spiral and its tangent (渦巻き上のある点と中心を結ぶ線とその点における接線の成す角)
この時、
k = 1 / tan (φ)
渦巻きが1本の場合: ρ = (a exp (kθ) ) / (a exp (k(θ+ 2π) ) = exp (-2πk)
渦巻きがn本の場合: ρ = ri / ri + 1 = ( a exp (k (θ+ 2π(i - 1) / n) ) ) / ( a exp (k (θ+ 2πi ) / n) ) ) = exp (-2πk / n)
よって、いずれの場合も: ρ = exp (-2πk / n)
という関係にある。すなわち、パラメータ k、φ、ρ については、1つが定まれば残りの2つも定まる。
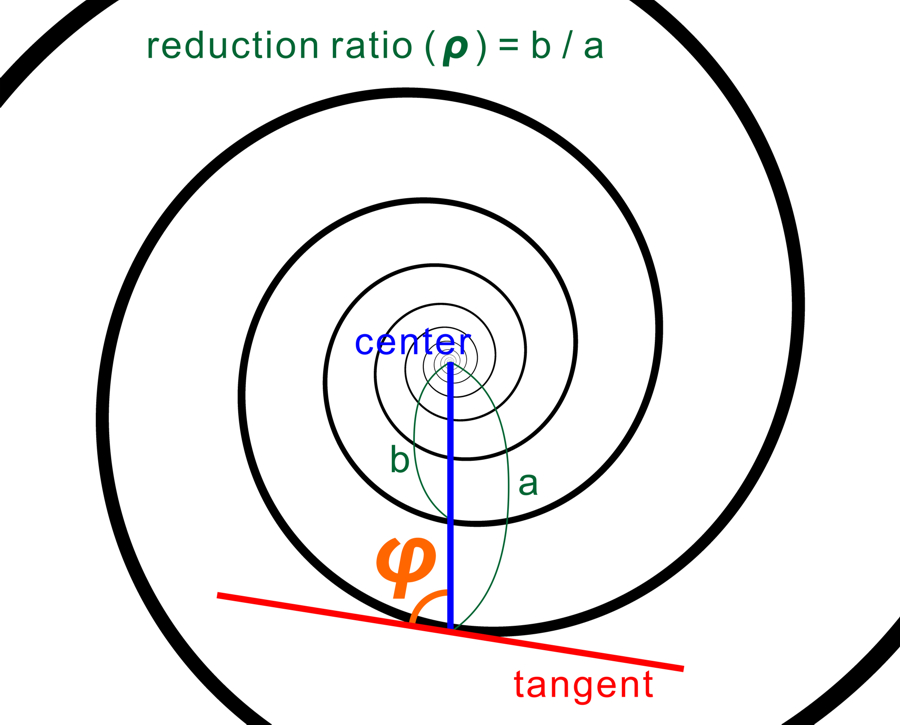
ρ = 60%, n = 2, φ = 81 deg
Click the image to download a high-resolution image (8000 x 8000 pixel)