Spirals
since January 15, 2016
Bernoulli's spiral: r = a exp (kθ) (ベルヌーイの渦巻き、ベルヌーイの螺旋、対数螺旋(logarithmic spiral)、等角螺旋(equiangular spiral)などと呼ばれる。ただし、螺旋は helix と対応する概念を表した用語と考えるのであれば誤訳であり、対数螺旋は対数的渦巻き、等角螺旋は等角的渦巻きと呼ぶべきかもしれない)
渦巻きが1本の場合: r = a exp (kθ)
渦巻きがn本の場合: r = (r1, r2, … ri, … rn)
ri = a exp (k(θ+ 2π(i - 1) / n) )
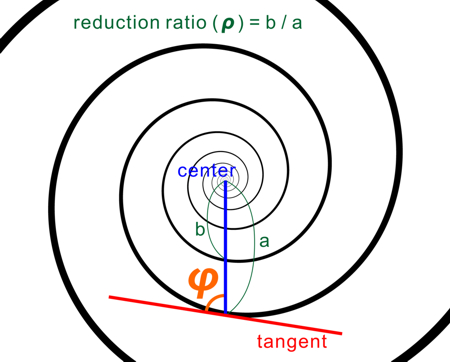
ρ: reduction ratio (縮小率), n: number of spirals (渦巻きの本数), phi (φ): angle between the line connecting the center with a particular point on a spiral and its tangent (渦巻き上のある点と中心を結ぶ線とその点における接線の成す角)
この時、
k = 1 / tan (φ)
渦巻きが1本の場合: ρ = (a exp (kθ) ) / (a exp (k(θ+ 2π) ) = exp (-2πk)
渦巻きがn本の場合: ρ = ri / ri + 1 = ( a exp (k (θ+ 2π(i - 1) / n) ) ) / ( a exp (k (θ+ 2πi ) / n) ) ) = exp (-2πk / n)
よって、いずれの場合も: ρ = exp (-2πk / n)
という関係にある。すなわち、パラメータ k、φ、ρ については、1つが定まれば残りの2つも定まる。
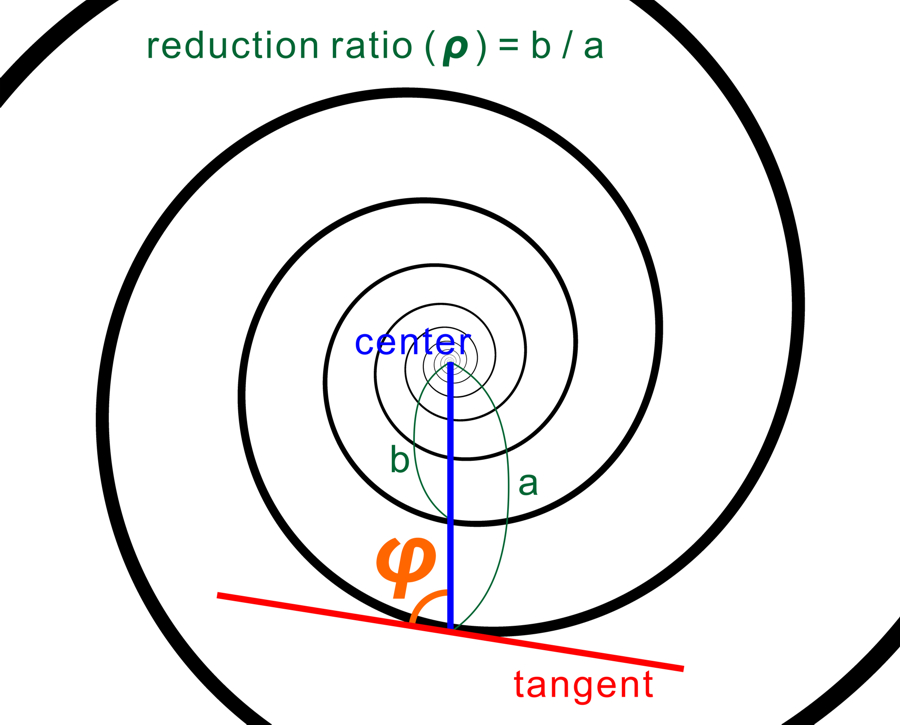
ρ = 60%, n = 2, φ = 81 deg

ρ = 90%, n = 10, φ = 80 deg

ρ = 90%, n = 5, φ = 80 deg

ρ = 90%, n = 1, φ = 89 deg

ρ = 90%, n = 0, φ = 90 deg (= concentric circle)

ρ = 90%, n = 15, φ = 76 deg

ρ = 90%, n = 20, φ = 71 deg

ρ = 90%, n = 25, φ = 67 deg

ρ = 90%, n = 30, φ = 63 deg

ρ = 90%, n = 60, φ = 45 deg

ρ = 90%, n = 120, φ = 26 deg

ρ = 80%, n = 10, φ = 70 deg

ρ = 70%, n = 10, φ = 60 deg

ρ = 60%, n = 10, φ = 51 deg

ρ = 40%, n = 1, φ = 82 deg

ρ = 90%, n = 10, φi = 80 deg

ρ = 90%, n = 10, φ = 80 deg

ρ = 80%, n = 5, φ = 80 deg
Circle: r = a
円が1つの場合: r = a
対数的同心円(logarithmic concentric circles)の場合: r = {… ri-1, ri, ri+1, …|i ∈ Z}
ri = a exp (2πki)
ベルヌーイの渦巻きと同様に、ρ: reduction ratio (縮小率) とすると、
ρ = (a exp (2πki) ) / (exp (2πk(i+1)) ) = exp (-2πk)
これは、n = 1 の時のベルヌーイの渦巻きの縮小率に等しい。
phi (φ): angle between the line connecting the center with a particular point
on a circle and its tangent (円上のある点と中心を結ぶ線とその点における接線の成す角)は常に90度。
φ = 90 deg
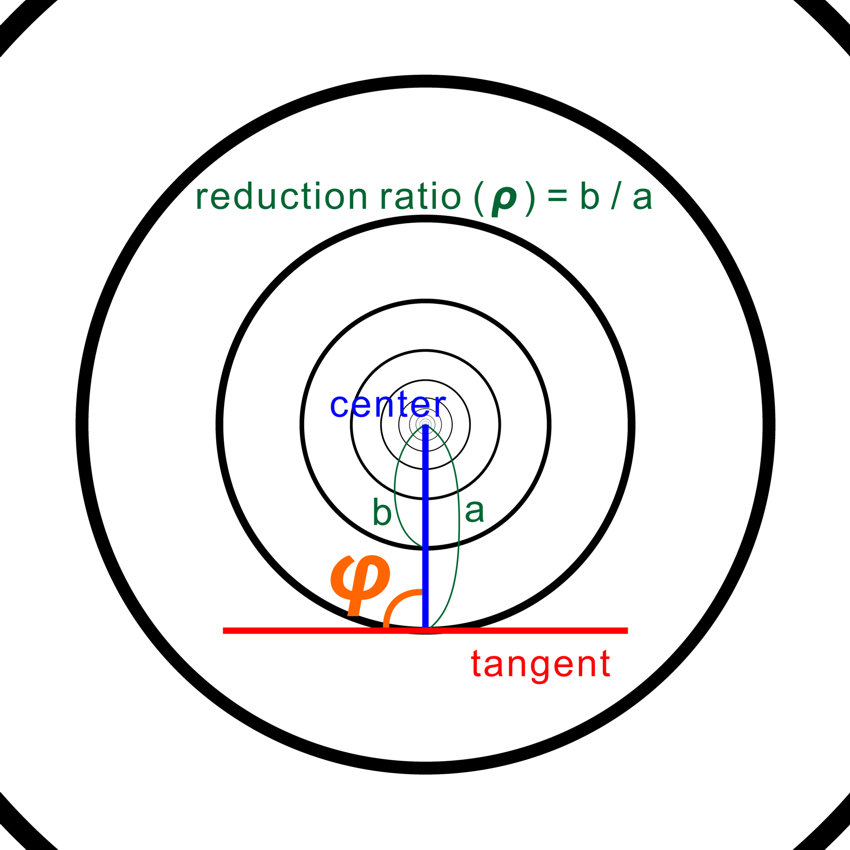
ρ = 60%, φ = 90 deg

ρ = 90% の対数的同心円
これは、ρ = 90%, n = 0, φ = 90 deg のベルヌーイの渦巻きと言うこともできる。

ρ = 50% の対数的同心円
これは、ρ = 50%, n = 0, φ = 90 deg のベルヌーイの渦巻きと言うこともできる。
放射パターンの数式はこうかな?
放射パターンが1本の場合: r = b, θ= c ただし、b ≥ 0 で不定、cは一定
放射パターンがn本の場合: r =(r1, r2, … ri, … rn)
ri = b, θ= c + 2π(i - 1) / n ただし、b ≥ 0 で不定、cは一定

n = 30 の放射パターン
これは、n = 30, φ = 0 deg のベルヌーイの渦巻きと言うこともできる。このとき、ρ = 0% と表現できるし、あるいは定義できないと表現するところと考えられる。

cf. ベルヌーイの渦巻き ρ = 46%, n = 30, φ = 15 deg

"Gravity wave spirals"
Concentric circles appear to be spirals that go to the center rotating clockwise.
Copyright Akiyoshi Kitaoka 2016 (February 13)
(No illusion if circles are homogeneously black or white)



"Gravity wave spirals: ρ = 90%"
Concentric circles appear to be spirals that go to the center rotating clockwise.
Copyright Akiyoshi Kitaoka 2017 (January 22)

"Gravity wave spirals: ρ = 85%"
Concentric circles appear to be spirals that go to the center rotating clockwise.
Copyright Akiyoshi Kitaoka 2017 (January 22)

"Gravity wave spirals: ρ = 80%"
Concentric circles appear to be spirals that go to the center rotating clockwise.
Copyright Akiyoshi Kitaoka 2017 (January 22)

"Gravity wave spirals: ρ = 75%"
Concentric circles appear to be spirals that go to the center rotating clockwise.
Copyright Akiyoshi Kitaoka 2017 (January 30)

"Gravity wave spirals: ρ = 70%"
Concentric circles appear to be spirals that go to the center rotating clockwise.
Copyright Akiyoshi Kitaoka 2017 (January 30)
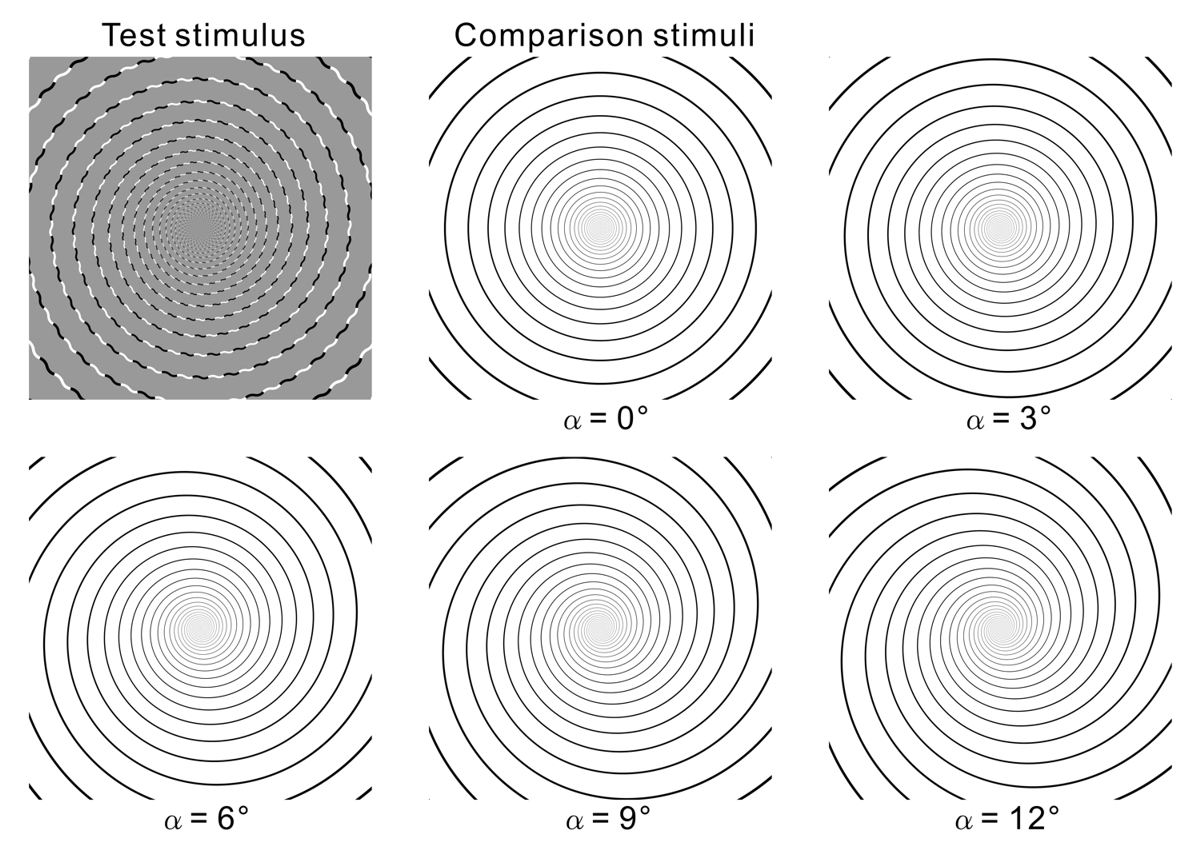
"How to measure the illusion magnitude of the spiral illusion"
α = 90° - φ, ρ = 85 %
Copyright Akiyoshi Kitaoka 2017 (January 22)
実験刺激の案

ρ = 85 %, counterclockwise expanding spiral illusion

ρ = 85 %, clockwise expanding spiral illusion
テスト用の渦巻き錯視の錯視量を測定して、テスト用渦巻き図形を選ぶ↓

α = 6°, ρ = 85 %, counterclockwise expanding spiral

α = 6°, ρ = 85 %, clockwise expanding spiral
順応法
渦巻き錯視図形
(1)渦巻きが反時計回りに回転して拡大して見える図形 → 渦巻きが時計回りに回転して拡大して見える図形
(2)渦巻きが時計回りに回転して拡大して見える図形 → 渦巻きが反時計回りに回転して拡大して見える図形
渦巻き図形
(1)渦巻きが反時計回りに回転して拡大する図形 → 渦巻きが時計回りに回転して拡大する図形
(2)渦巻きが時計回りに回転して拡大する図形 → 渦巻きが反時計回りに回転して拡大する図形
regular image vs. mirror image とかの名称にするべきか?