
錯覚の解明・創作・応用への諸アプローチ 第16回錯覚ワークショップ
2022年3月2日(水)15:20~16:00
傾き錯視と同居する静止画が動いて見える錯視の探求
立命館大学総合心理学部 北岡 明佳 email 2022/2/26 より
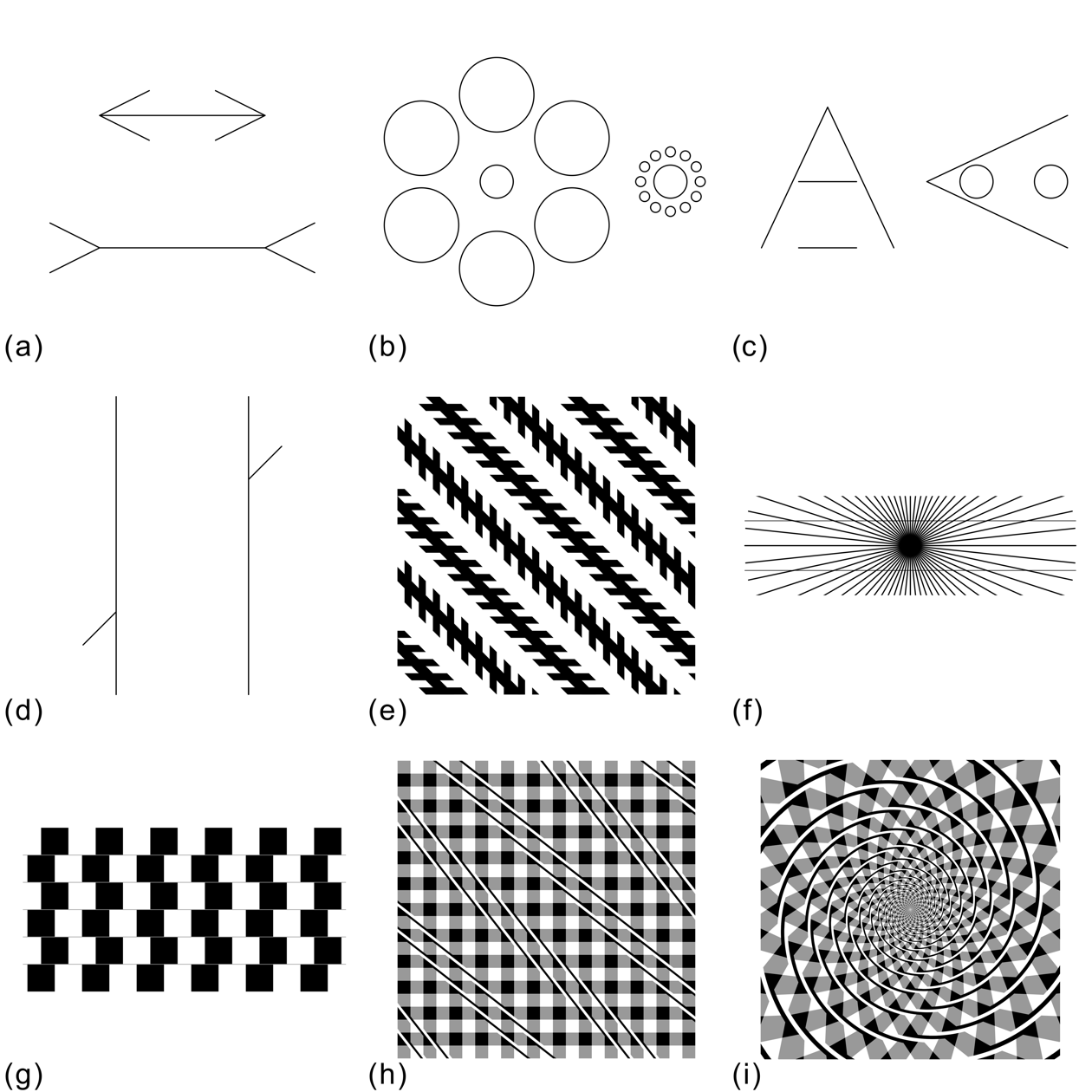
古典的な幾何学的錯視の例。(a)ミュラー=リヤー錯視。上下の水平線分は同じ長さであるが、下の方が長く見える。(b)エビングハウス錯視。リングの中の円は左右同じ大きさであるが、大きい円のリングに囲まれた左の円よりも、小さい円のリングに囲まれた右の円の方が大きく見える。(c)ボンゾ錯視。Λや<の頂点に近い方に置かれた対象が大きく見える。具体的には、2本の水平線分は同じ長さだが、上の方が長く見える。2つの円は同じ大きさだが、左の方が大きく見える。(d)ポッゲンドルフ錯視。2つの斜線は一直線上にあるが、右の斜線の方が上方に変位して見える。(e)ツェルナー錯視。垂直より反時計回りに45度傾いた黒い線は互いに平行だが、交互に傾いて見える。交差する短い線との交差角度の過大視の現象である。(f)へリング錯視(湾曲錯視)。水平線分が曲がって見える。上の線分は上に凸、下の線分は下に凸に見える。(g)ミュンスターベルク錯視。白と黒の正方形の列を図のようにずらして配置し、列の境界に線分を描くと、図ではそれらは水平であるが、交互に傾いて見える。本図のように線が灰色の時は、カフェウォール錯視(Café Wall illusion)と呼ばれることが多い。(h)フレーザー錯視。垂直より反時計回りに45度傾いた仮想線に沿って短い斜線の列が描かれているが、列の傾きは短い斜線の傾きの方向に変位して見える。ツェルナー錯視とは逆の錯視である。(i)フレーザー錯視の渦巻き錯視。フレーザー錯視では、傾いて見えるのは線分であるが、傾いて見える対象を円状に配置した時に観察できる錯視である。具体的には、同心円が渦巻きのように見える。
Kitaoka, A. (2010) Tilt illusions and anomalous motion illusions. (talk in the RIKEN BSI on July 2, 2010) Presentation (html)
Tilt illusion is a subcategory of geometrical illusion, in which lines or edges appear to tilt clockwise or counterclockwise. (e.g., Zöllner illusion, Fraser illusion, Café Wall illusion)
Anomalous motion illusion refers to motion illusion in a stationary image, in which part of the
stationary image appears to move. (e.g., Ouchi illusion, Enigma illusion,
optimized Fraser-Wilcox illusion)
Some* types of tilt illusions are accompanied by anomalous motion illusion. (e.g., Illusion of Y-junctions)
*Later, I have realized that most of tilt illusions (including the Fraser illusion and the Café Wall illusion) share the same image with anomalous motion illusion.

"The autumn color swamp"
The inset appears to move.
Copyright A.Kitaoka 2000, 2003, 2007, 2010
<Handout>

The two concentric arrays of stars appear to rotate in the different directions when we approach or move away from the figure while fixating at the center.
Copyright Akiyoshi Kitaoka 2000, 2010
<Handout>
Illusion of Y-junctions
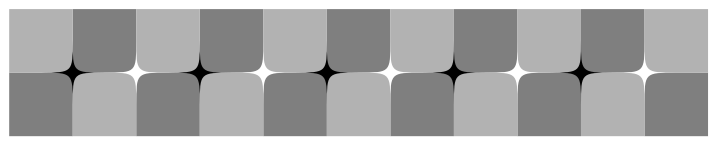
The elemental image as the tilt illusion
The horizontal edge on which black or white stars are placed appears to tilt counterclockwise.
Kitaoka, A., Pinna, B., and Brelstaff, G. (2001). New variations of spiral
illusions. Perception, 30, 637-646.
Kitaoka, A., Pinna, B., and Brelstaff, G. (2004). Contrast polarities determine the direction of Cafe Wall tilts. Perception, 33, 11-20.

The elemental image as anomalous motion illusion
The inset appears to move. When the retinal image is moved vertically, the inset appears to move horizontally. When the retinal image is moved horizontally, the inset appears to move vertically.
<Handout>
Today's talk
1. "Discovery" of the Fraser illusion family
2. Anomalous motion illusion accompanied by tilt illusion
3. A speculation of the "Rotating snakes" illusion
§1. "Discovery" of the Fraser illusion family

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.

Fraser's spiral
(spiral illusion of the Fraser illusion)
Concentric circles of "twisted cords" appear to be spirals.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
<Handout>

In December 2009, I developed a "new" illusion (though it essentially was not new), which I called the "pseudo Fraser illusion".

"Pseudo Fraser
spirals"
Concentric rings appear to be spirals.
Copyright Akiyoshi Kitaoka 2009 (December 17)

Psudo-Fraser illusion
("Fraser's Café Wall" illusion)
The middle lines are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)

Pseudo-Fraser's spiral
(spiral illusion of the "Fraser Café Wall" illusion)
Concentric circles of "twisted cords" appear to be spirals.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Q. What are the differences between the Fraser illusion and the pseudo-Fraser illusion?
A. There are three factors involved:
1. whether the inducers are obliques (Fraser illusion) or not (pseudo-Fraser illusion)
2. whether the inducers are only lines (Fraser illusion) or combination of lines and edges (pseudo-Fraser illusion)
3. whether the inducers are two (Fraser illusion) or four (pseudo-Fraser illusion)
1. whether the inducers are obliques (Fraser illusion) or not (pseudo-Fraser illusion)
Finding: There are counterparts of the Fraser illusion as well as the pseudo-Fraser illusion, respectively

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
The counterpart of the Fraser illusion

Illusion of shifted lines
Rows of middle line segments are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Kitaoka, A. (2007) Tilt illusions after Oyama (1960): A review. Japanese Psychological Research, 49, 7-19.

Psudo-Fraser illusion
("Fraser's Café Wall" illusion)
The middle lines are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
The counterpart of the pseudo-Fraser illusion

The patterns like "twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
2. whether the inducers are only lines (Fraser illusion) or combination of lines and edges (pseudo-Fraser illusion)
Finding: There are three groups in this sense, only lines, combinations of lines and edges, and only edges, respectively
Lines only

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
Combination of lines and edges

"Cafe Wall Fraser" illusion
The patterns like "twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
Edges only

Illusion of oblique edges
Rows of oblique edges are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Kitaoka, A. (2007) Tilt illusions after Oyama (1960): A review. Japanese Psychological Research, 49, 7-19.
3. whether the inducers are two (Fraser illusion) or four (pseudo-Fraser illusion)
Finding: The basic components of the Fraser illusion can be counted four to match the pseudo-Fraser illusion. In the same way, The basic components of the pseudo-Fraser illusion can be counted two to match the Fraser illusion. Thus, this factor is not essential for tilt illusion.

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
The counterpart of the Fraser illusion

Fraser illusion
"Twisted cords" are horizontally aligned but appear to tilt alternately. The apparent tilt is the same orientation as the tilt of each obliques.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.

Psudo-Fraser illusion
("Fraser's Café Wall" illusion)
The middle lines are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
The counterpart of the pseudo-Fraser illusion

Psudo-Fraser illusion
("Fraser's Café Wall" illusion)
The middle lines are horizontally aligned but appear to tilt alternately. The apparent tilt is counterclockwise, clockwise, and so on from the top row.
Drawn by Akiyoshi Kitaoka 2010 (March 20)
cf. Fraser, J. (1908) A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
Conclusion: The Fraser illusion family consists of six (3 x 2) illusions.
<Handout>
Q. How is the pseudo-Fraser illusion related to the Café Wall illusion?
A. I think they are essentally the same illusion.


The pseudo-Fraser illusion (left) and the Café Wall illusion (right)

Café Wall illusion: a standard image
cf. Gregory, R. L. and Heard, P. (1979) Border locking and the Café Wall illusion. Perception, 8, 365-380.
Q. Does tilt illusion occur where contast polarity changes?
A. Yes, as if it were the reversed phi (the direction opposite to the shift).
(Illusion of oblique edges)
(Illusion of shifted lines)
Example

"Derby man tilt illusion"
Horizontally aligned rows of "derby men" appear to tilt alternately. From the top, counterclockwise, clockwise, and so on.
Copyright Akiyoshi Kitaoka 2010 (March 21)
My idea: There are eight fundamental combinations of basic components.
(I imagine that neurons with receptive fields like these play a part)
(The limiting case of the Fraser illusion family)
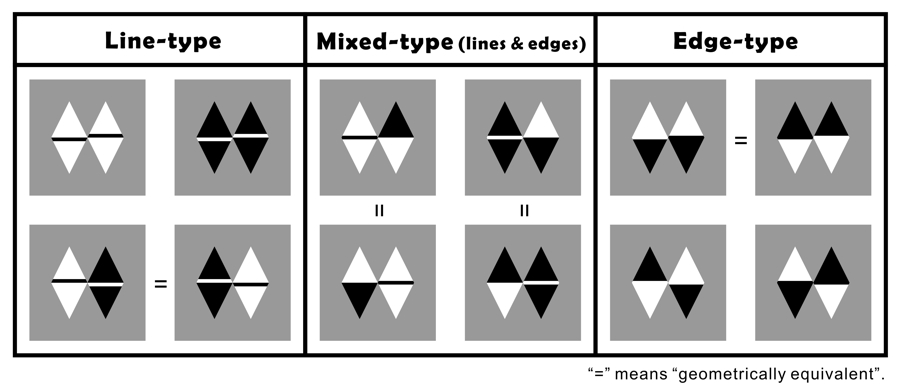
In each gray square, the middle line or edge appears to tilt counterclockwise.
Copyright Akiyoshi Kitaoka 2010 (March 22)
In addition: Café Wall illusion can be explained with this idea.

Café Wall illusion: a standard image
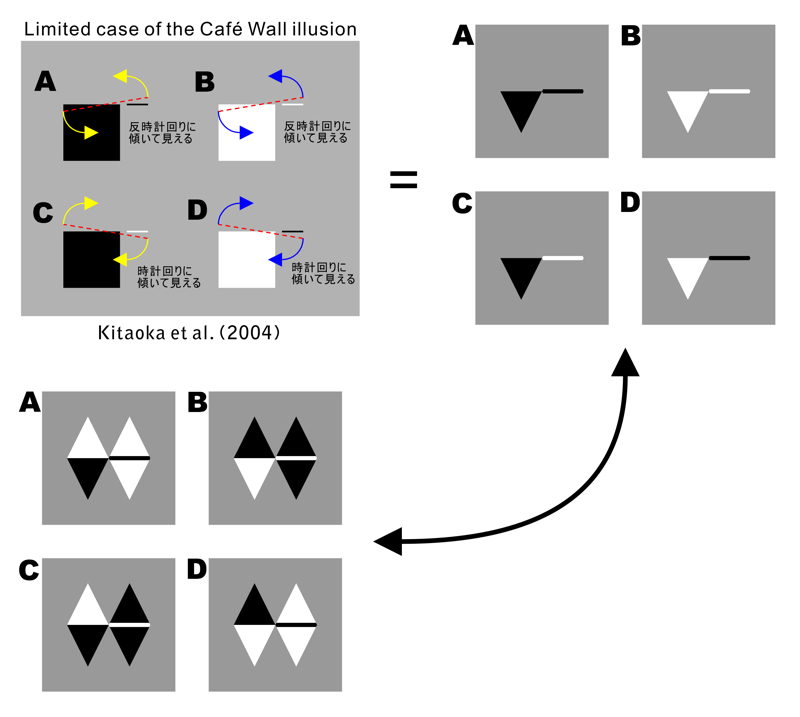
Copyright Akiyoshi Kitaoka 2010 (March 22)
Kitaoka, A., Pinna, B., and Brelstaff, G. (2004) Contrast polarities determine the direction of Café Wall tilts. Perception, 33, 11-20.
Kitaoka, A. (2010). The Fraser illusion family and the corresponding motion illusions. 33rd European Conference on Visual Perception (ECVP 2010), EPFL, Lausanne, Switzerland, 2010/8/22-26, 8/26 poster publication. Poster (Kitaoka, A. (2010) The Fraser illusion family and the corresponding motion illusions. Perception, 39, Supplement, #61, p. 178)
§2. Anomalous motion illusion accompanied by tilt illusion

"Obake-hime"
obake = ghost; hime = princess or girl
The face appears to expand; the group of bats appears to rotate counterclockwise. This is Professor Mather's four-stroke motion.
Copyright Akiyoshi Kitaoka 2009 (August 10)
Professor Mather's demonstration is the best.
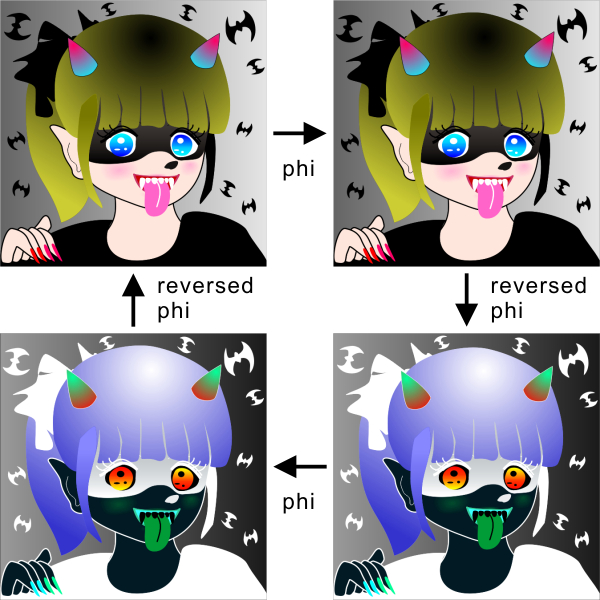
Copyright Akiyoshi Kitaoka 2010 (March 22)
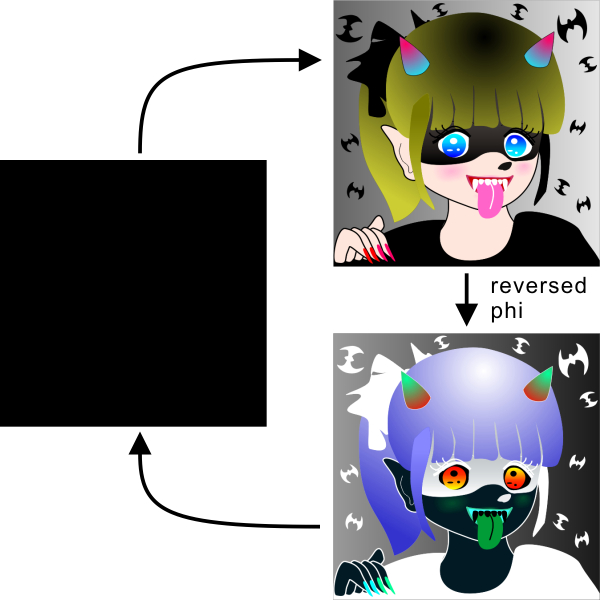
(Reversed phi only)

Copyright Akiyoshi Kitaoka 2010 (March 22)
Reversed phi movement (Anstis and Rogers 1975). There are four rectangles, each of which is flanked by thin lines that are dark or light. When the luminance of the rectangles decreases and that of the background increases accordingly, the upper two appear to converge in motion while the lower two appear to go apart in motion. On the other hand, when the luminance of the rectangles increases and that of the background decreases accordingly, the upper two appear to go apart in motion while the lower two appear to approach each other in motion. In sum, the direction of apparent motion is from the dark flank to the neighboring part that goes darkening or from the light flank to the neighboring part that goes brightening. Although the rectangles are aligned vertically, the apparent positional displacement occurs in the opposite direction to motion. If observers cross-fuse (uncross-fuse) the right and left rectangles, the upper rectangle appears to be in front of (behind) the lower one when they are dark.
Kitaoka, A. (2006) Configurational coincidence
among six phenomena: A comment on van Lier and Csathó (2006). Perception,
35, 799-806. animations ![]()
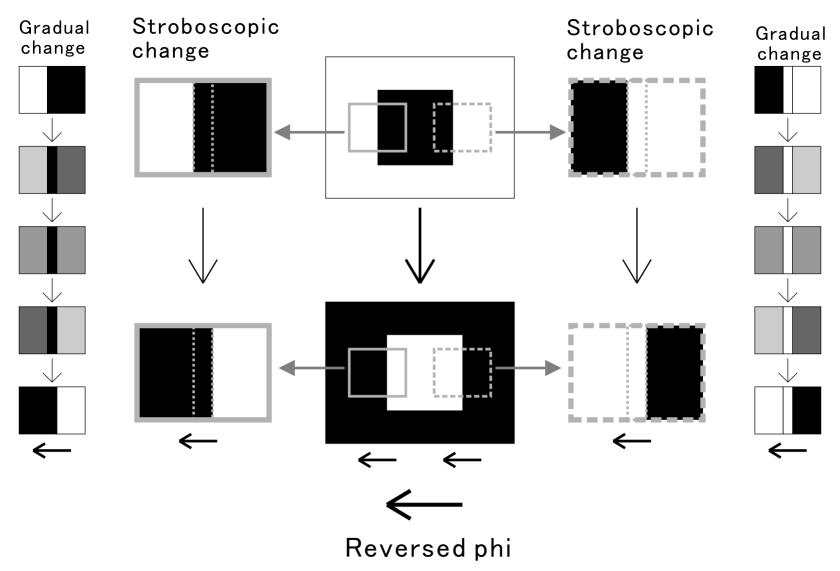
Anstis S M, 1970 “Phi movement as a subtraction process” Vision Research 10 1411-1430
Anstis S M, Rogers B J, 1975 “Illusory reversal of visual depth and movement during changes of contrast” Vision Research 15 957-961
4-stroke motion corresponding to the Line Type

Copyright Akiyoshi Kitaoka 2010 (March 22)

Finding: The direction of motion is the same as the tilt illusion.
Mather, G. and Murdoch, L. (1999) Second-order processing of four-stroke apparent motion. Vision Research, 39, 1795-1802.
cf. van Lier R, Csathó Á, 2005 “Dancing shapes: A comparison of luminance induced distortions” Perception, 35, 775 – 798.
4-stroke motion corresponding to the Edge Type

Copyright Akiyoshi Kitaoka 2010 (March 22)

Finding: The direction of motion is the same as the tilt illusion.
cf. van Lier R, Csathó Á, 2005 “Dancing shapes: A comparison of luminance induced distortions” Perception, 35, 775 – 798.
4-stroke motion corresponding to the Mixed Type

Copyright Akiyoshi Kitaoka 2010 (March 22)

Finding: The direction of motion is the same as the tilt illusion.
<Takeuchi's four-stroke motion>
Takeuchi, T. (1997) The motion analogue of the cafe wall illusion. Perception, 26, 569-584.
Then, anomalous motion illusions that coexist in tilt illusion images can be explained in this context.
When the retinal image slides in the special direction, the orientation along which the tilt illusion occurs, the four-stroke motion is induced and anomalous motion illusion is observed.
Copyright Akiyoshi Kitaoka 2010 (June 26)
<Handout>

"Rain"
The inset appears to move.
Copyright Aliyoshi Kitaoka 2005 (July 2)
Explanation of the illusion of Y-junctions

Drawn by Aliyoshi Kitaoka 2010 (June 25)

(Takeuchi's four-stroke motion)
<Two dimensional displays>

Illusion of Y-junctions
Kitaoka, A., Pinna, B., and Brelstaff, G. (2001). New variations of spiral
illusions. Perception, 30, 637-646.
Kitaoka, A., Pinna, B., and Brelstaff, G. (2004). Contrast polarities determine the direction of Cafe Wall tilts. Perception, 33, 11-20.


Pinna Illusion
Pinna, B. and Brelstaff, G. J. (2000) A new visual illusion of relative motion. Vision Research, 40, 2091-2096.
Explanation of the Pinna illusion
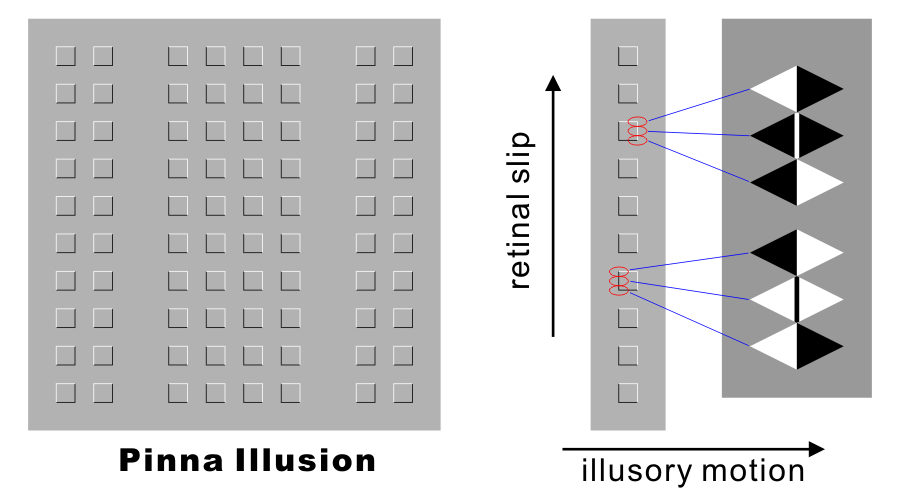
New: This idea led me to produce a novel illusion "spine drift illusion".
"Spine drift
illusion"
The inset appears to move.
Copyright Akiyoshi Kitaoka 2010 (June 4)

"Spine drift illusion"
The inset appears to move.
Copyright Akiyoshi Kitaoka 2010 (July 6)
<Handout>
"Spine drift
illusion with the illusion of shifted lines"
The inset appears to move.
Copyright Akiyoshi Kitaoka 2010 (June 5)
"Hamburger drift
illusion"
The inset appears to move.
Copyright Akiyoshi Kitaoka 2010 (June 6)
Gabor patches with a special carrier/envelope ratio render anomalous motion illusion.

Gabor patch drift illusion (Gurnsey-Morgan illusion)
The inset appears to move.
Drawn by Akiyoshi Kitaoka 2007 (August 8)
<Handout>
cf. Popple illusion (phase-shift illusion)

Popple, A. V. and Levi, D. M. (2000) A new illusion demonstrates long-range
processing. Vision Research, 40, 2545-2549.
Popple, A. V. and Sagi, D. (2000) A Fraser illusion without local cues?
Vision Research, 40, 873-878.

「エンボスドリフト錯視」
(サイン波型)
内側の正方形領域が動いて見える。
"Drifting Emboss illusion"
(sine type)
The inset appears to move.
Copyright Akiyoshi Kitaoka 2016 (February 15)
北岡明佳 (2021) 「輝度変化による運動錯視(リバースファイなど)の再検討」 (2021年3月2日(火)15:40~16:20・第15回錯覚ワークショップ(Zoom Webinar)) Presentation (html)

「扉を開けたまま走る電車」
停車中の電車が右に走行するように見える。
Copyright Akiyoshi Kitaoka 2021 (February 9)
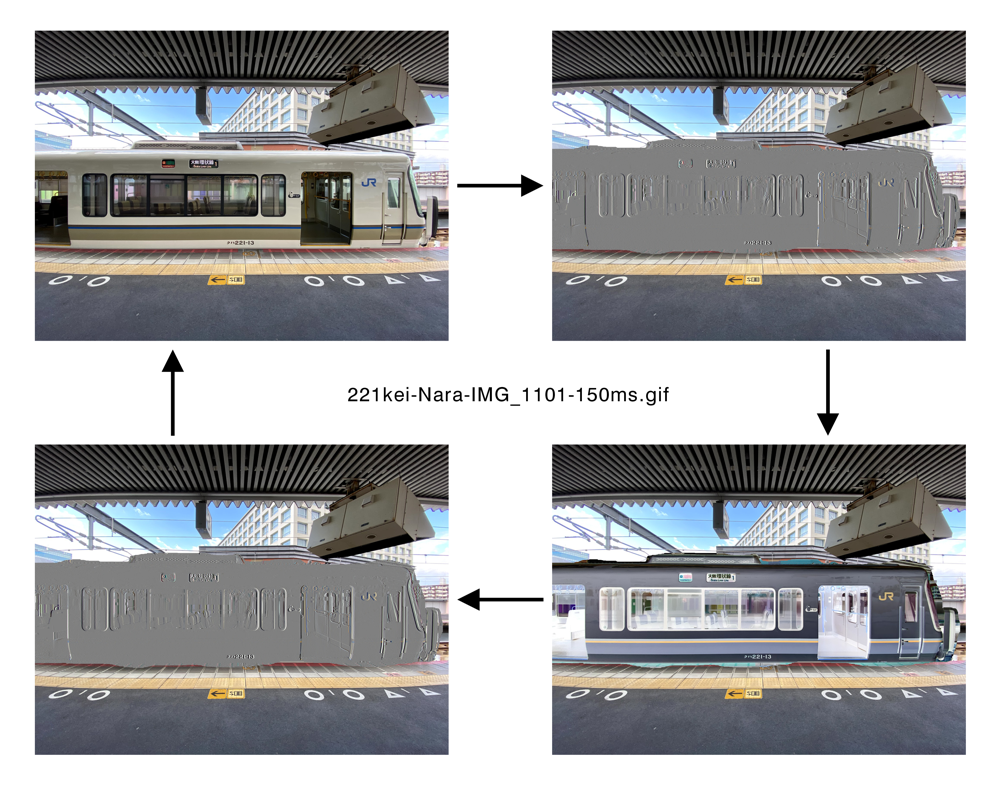
.gif)
停車中の電車が左に走行するように見える。

(運動残効確認用)

100 ms /frame
「電車のシーンの4ストローク運動(すべてリバースファイ)デモ」
(反転画像は、オリジナル動画の2フレーム目)
この動画はたった4枚の画像でできているが、電車は常に進行しているように見える。
Copyright Akiyoshi Kitaoka 2020 (March 22)
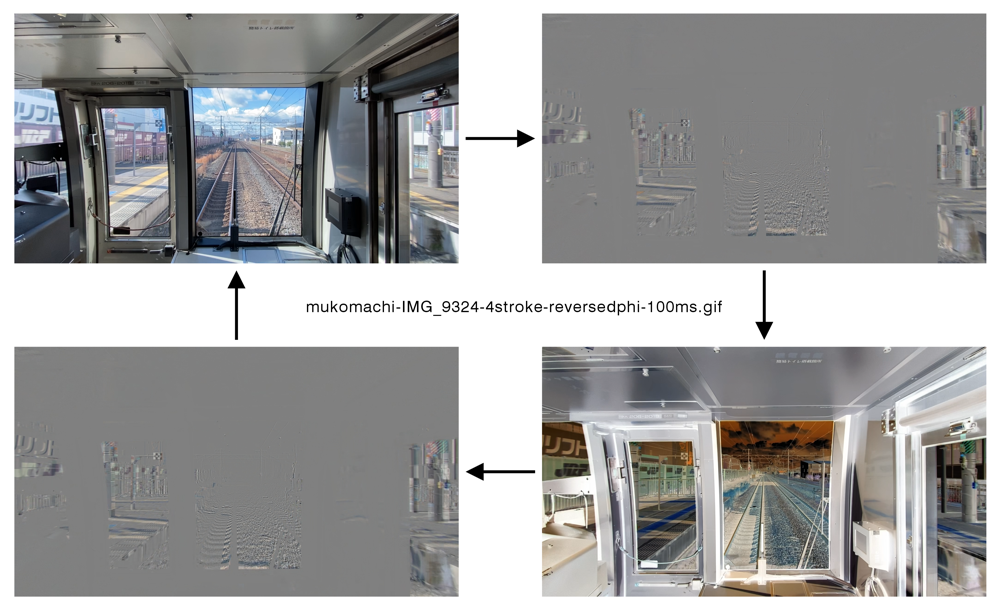

100 ms/frame
「電車のシーンの(マーザーの)4ストローク運動デモ」
この動画はたった4枚の画像でできているが、電車は常に進行しているように見える。
Copyright Akiyoshi Kitaoka 2020 (March 12)
Reference: http://www.georgemather.com/MotionDemos/FourstrokeMP4.html
Mather, G. and Murdoch, L. (1999) Second-order processing of four-stroke apparent motion. Vision Research, 39, 1795-1802.

本講演で紹介する「無限運動」は以下のように作る。
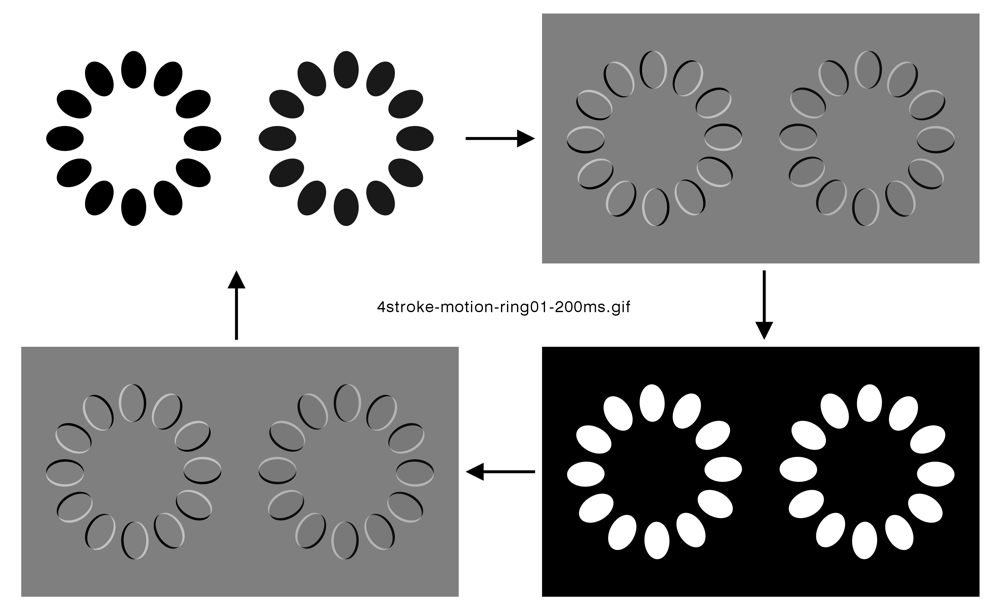
左上は1枚目の画像。右下は2枚目の画像をネガポジ反転させたもの。右下の画像では、左上の画像に比べて、左のリングは2度反時計回りに回転し、右のリングは2度時計回りに回転させている。右上と左下の画像は、左上と右下の画像の差分の画像である。
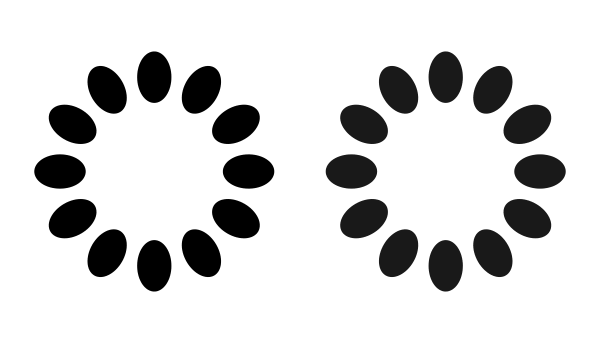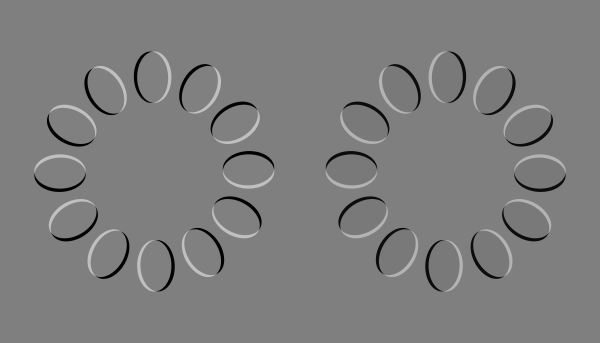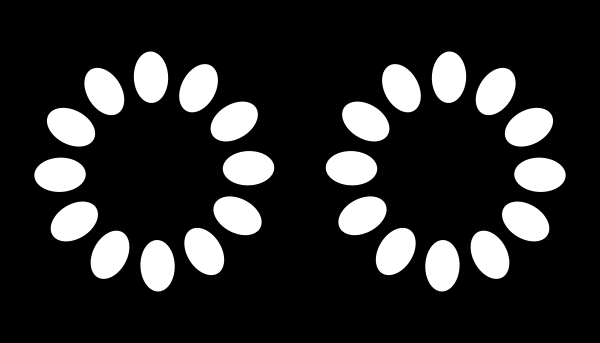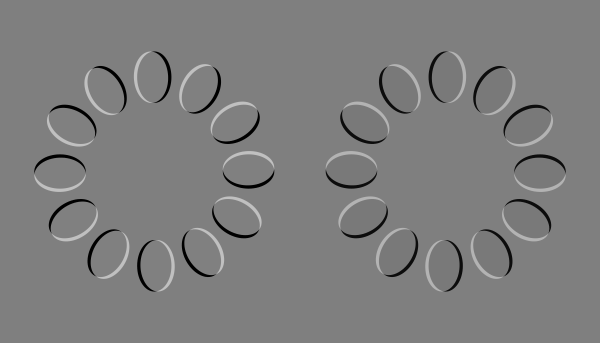
左のリングは反時計回りに、右のリングは時計回りに回転して見える。(200 ms / frame)
Copyright Akiyoshi Kitaoka 2021 (February 22)

背景を灰色に固定しても、この錯視は見える。(200 ms / frame)
Copyright Akiyoshi Kitaoka 2021 (February 22)
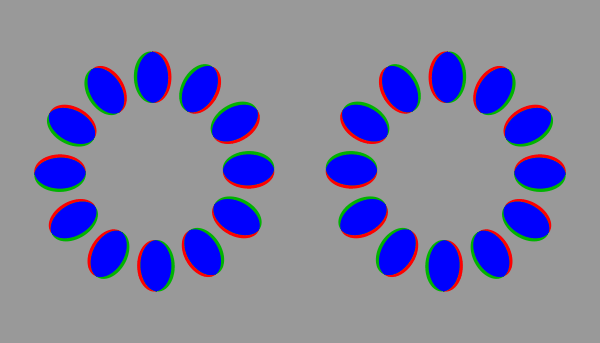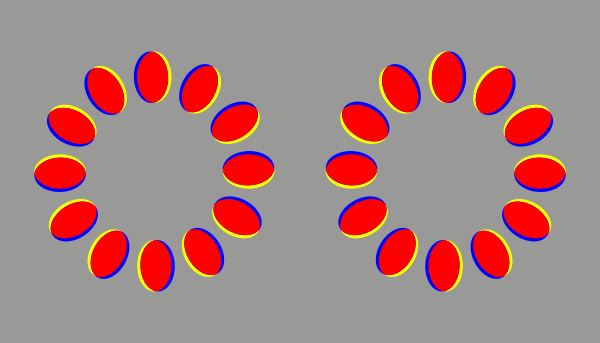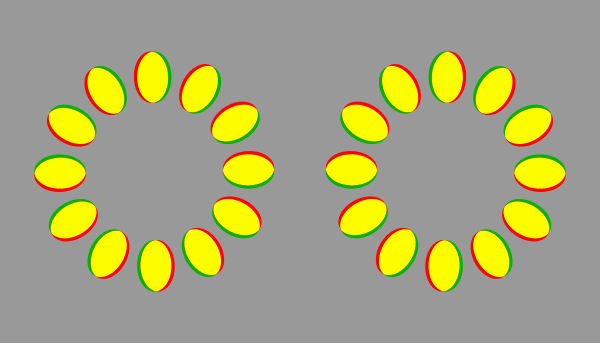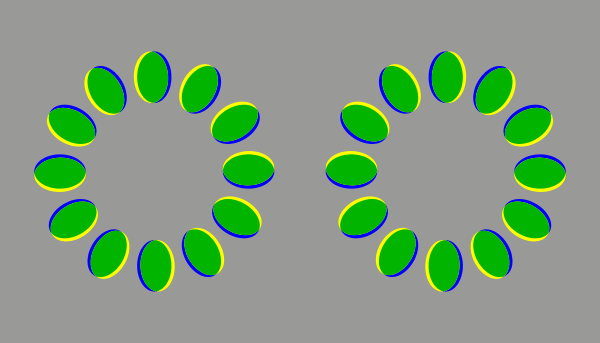
輝度の順番を変えずに色を付けても、この錯視は見える。(200 ms / frame)
Copyright Akiyoshi Kitaoka 2021 (February 22)
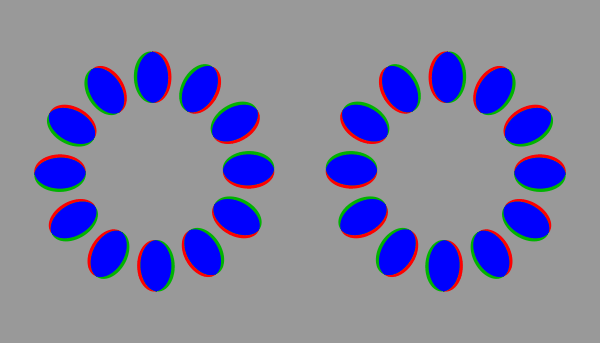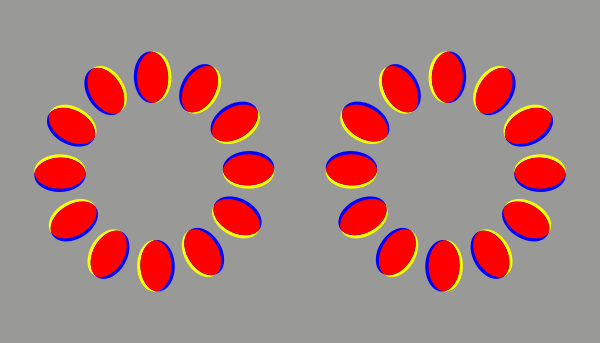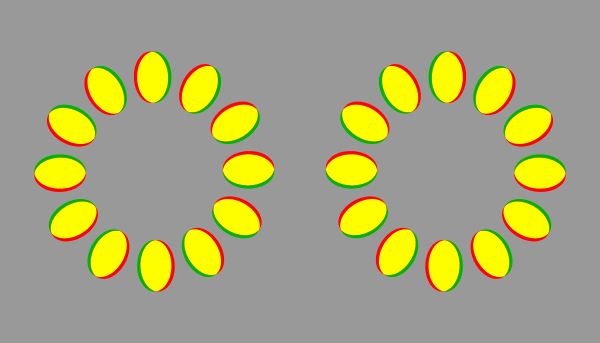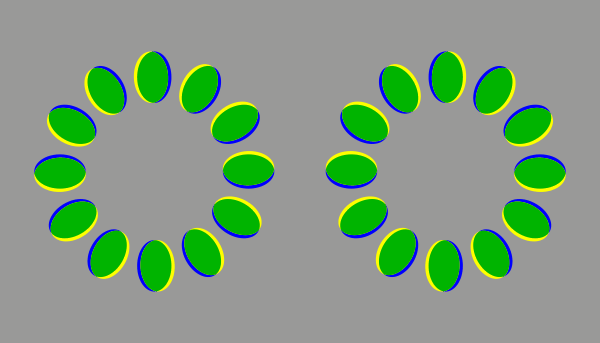
(100 ms / frame)
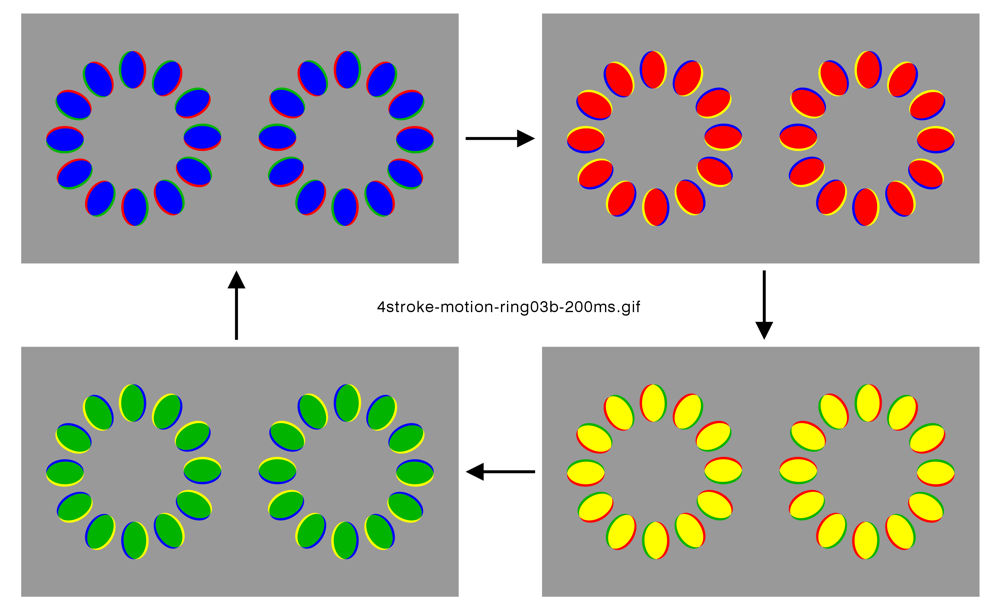
青は黒、黄は白、赤と緑は灰色に相当する。じゃがりきん氏の錯視作品を説明する原理である。ただし、じゃがりきん氏の作品では、色はなめらかに推移する。
Copyright Akiyoshi Kitaoka 2021 (February 22)
「無限運動錯視」を最初に提案したのは誰か?
普通に考えれば、Mather の four-stroke apparent motion であろうか? 論文は1999年に出ているが、その数年前には学会発表等でデモされていたと思われる(いずれMather先生に伺おうと思います)。
Reference: http://www.georgemather.com/MotionDemos/FourstrokeMP4.html
Mather, G. and Murdoch, L. (1999) Second-order processing of four-stroke apparent motion. Vision Research, 39, 1795-1802.

ツイッターで無限運動錯視を有名にしたのは、じゃがりきん氏。この数年のことと思われる(いずれじゃがりきん氏に伺おうと思います)。
スーパー錯視ブラザーズ pic.twitter.com/bLkFhBOCeU
— じゃがりきん (@jagarikin) November 20, 2020
https://nlab.itmedia.co.jp/nl/articles/2011/23/news016.html
筆者の最古の無限運動錯視デモは、2010年4月のようである。本日発表している形態のデモである。
最古の無限運動錯視デモの掲載されているウェブページ → movie7.html (ページの空白部分は、見れなくなった Flash デモがあるところ)
その動画 → Edgetype4strokemotion2.gif (どきついので、閲覧注意)
Anstis のスポーク車輪錯視(illusory totation of a spoked wheel)は、論文は2011年、学会発表は2000年頃らしい。

「スポーク車輪錯視(spoked wheel illusion)の再現」
灰色のスポークは静止しているが、背景の5方向の放射パターンが時計回り回転するのに対して、反時計回りに回転して見える。この運動残効は、5方向放射パターンの実運動の反対方向ではなく、灰色のスポークの錯視的運動の反対方向に起こる(Anstis & Rogers, 2011)。
Copyright Akiyoshi Kitaoka 2021 (February 13)
Anstis, S. M. & Rogers, B. (2011). Illusory rotation of a spoked wheel. i-Perception, 2, 720–723. https://doi.org/10.1068/i0483
Reverse Spoke Illusion from Michael Bach https://michaelbach.de/ot/mot-spokes/index.html
For the positive motion aftereffect, see
Nishida, S. & Sato, T. (1992). Positive motion after-effect induced by bandpass-filtered random-dot kinematograms. Vision Research, 32, 1635-1646. https://www.sciencedirect.com/science/article/pii/004269899290156D?via%3Dihub
スポーク車輪錯視には先代があった。「竹内の錯視」(論文は1997年)

「竹内のカフェウォール錯視の運動類似物錯視の再現」
灰色のスポークは静止しているが、背景の白黒の放射パターンが時計回り回転するのに対して、反時計回りに回転して見える。この運動残効は、放射パターンの実運動の反対方向ではなく、灰色のスポークの錯視的運動の反対方向に起る(Takeuchi, 1997)。
Copyright Akiyoshi Kitaoka 2021 (February 13)
Takeuchi, T. (1997) The motion analogue of the café wall illusion. Perception, 26, 569-584. https://doi.org/10.1068/p260569
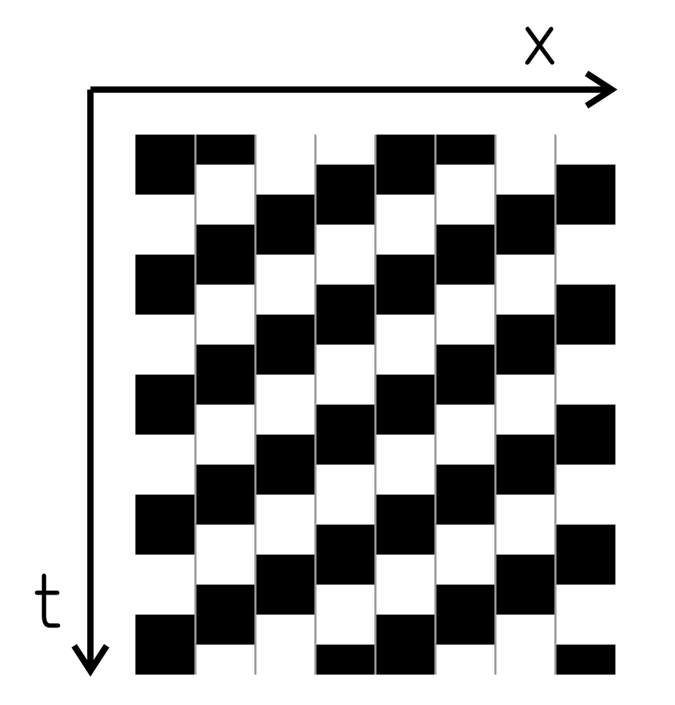
Takeuchi (1997) が指摘した灰色の線が動いて見える錯視とカフェウォール錯視(上図では、垂直の灰色の線が反時計回りに傾いて見える)との類似性
Copyright Akiyoshi Kitaoka 2021 (February 23)

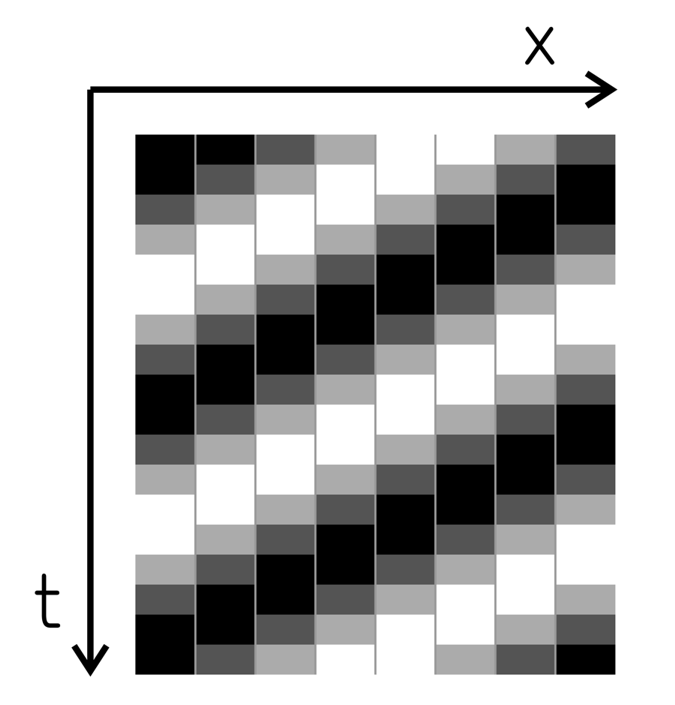
スポーク車輪錯視とカフェウォール錯視に似た錯視(ずれたグラデーションの錯視)(Kitaoka, 1998)(上図では、垂直の灰色の線が反時計回りに傾いて見える)との類似性
Kitaoka, A. (1998). Apparent contraction of edge angles. Perception, 27, 1209-1219. https://journals.sagepub.com/doi/10.1068/p271209
Copyright Akiyoshi Kitaoka 2021 (February 23)

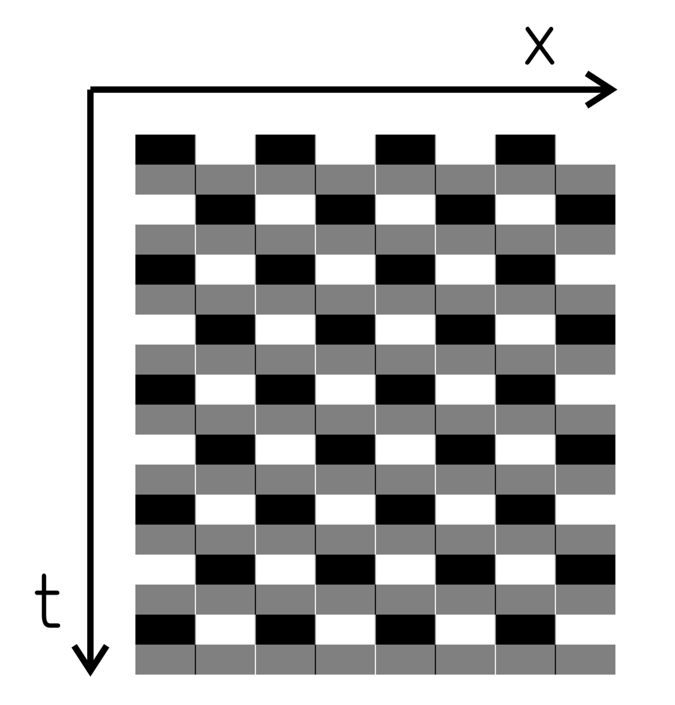
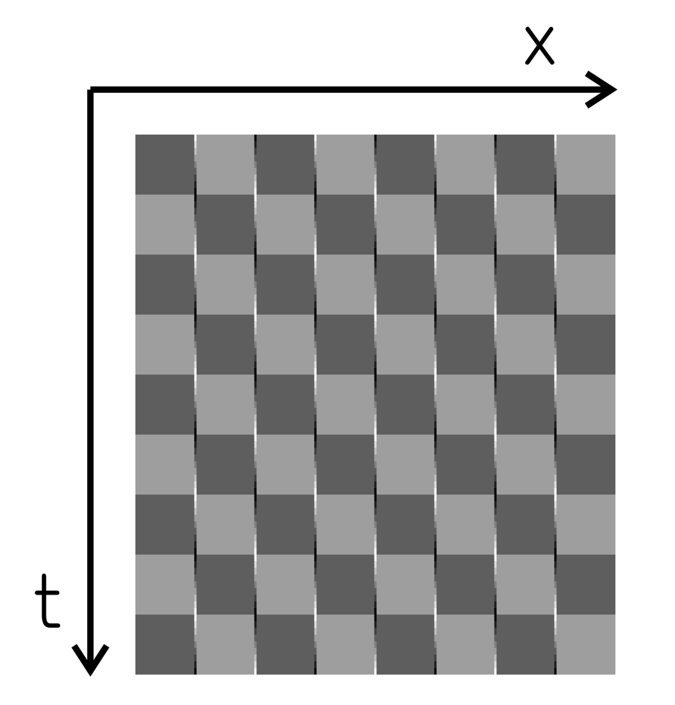
4フレームのリバースファイの「無限運動」と市松模様錯視(Kitaoka, 1998)(上図では、垂直の線分列が反時計回りに傾いて見える)との類似性

Copyright Akiyoshi Kitaoka 2021 (February 24)

Copyright Akiyoshi Kitaoka 2021 (February 11)
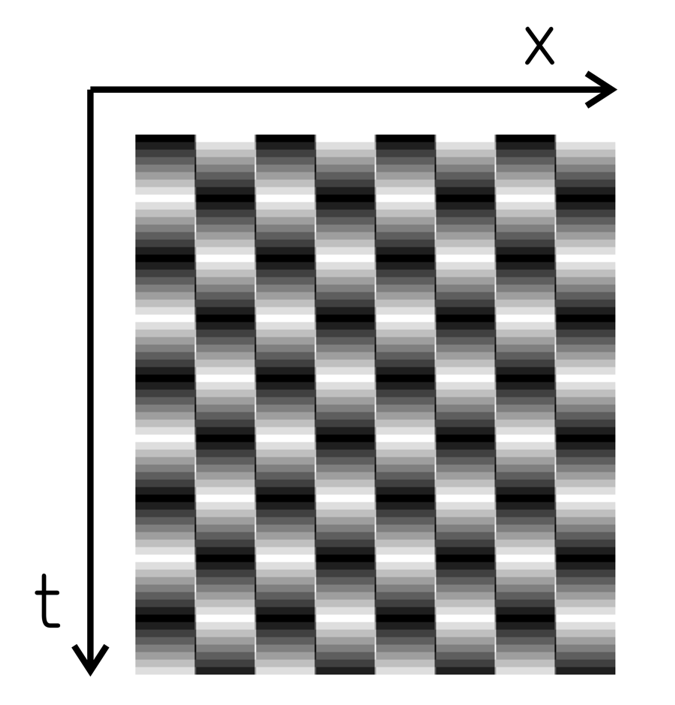
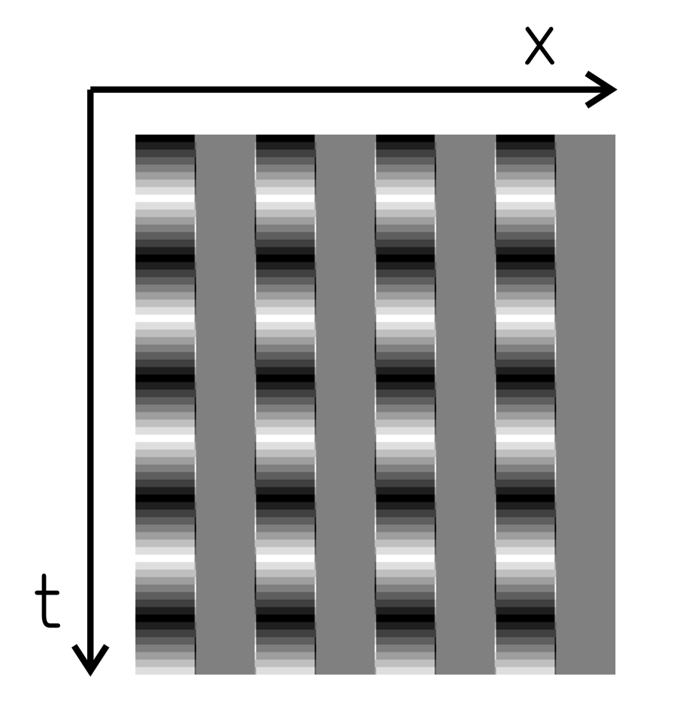
16フレームのリバースファイの「無限運動」と「メタルウォール錯視」(Kitaoka, 2010)(上図では、垂直の輝度勾配のある細い線が反時計回りに傾いて見える)との類似性

Copyright Akiyoshi Kitaoka 2021 (February 24)
cf.
突然ですが回転させると大きさが変化して見えるリングを考案しました pic.twitter.com/4GgHO7LHeF
— じゃがりきん (@jagarikin) February 19, 2020

Copyright Akiyoshi Kitaoka 2021 (March 1)
ところで、Mather の 4-stroke apparent motion には、どういう傾き錯視が対応するか?
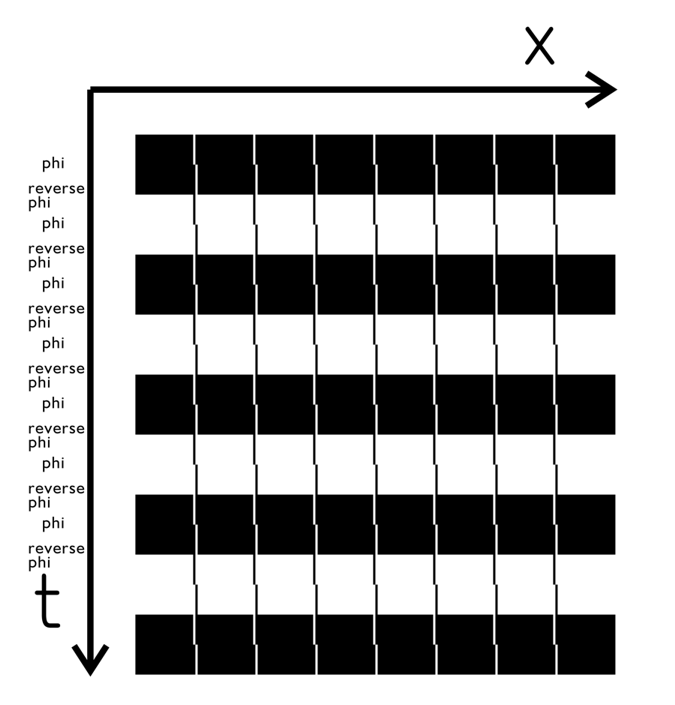
4ストローク運動とフレーザー錯視*との類似性
*この形態は「ずれた線の錯視」(illusion of shfted lines)(Kitaoka, 2007)(上図では、垂直に配列したずれた線分列が反時計回りに傾いて見える)である。


Fraser, J. (1908). A new visual illusion of direction. British Journal of Psychology, 2, 307-320.
https://bpspsychub.onlinelibrary.wiley.com/doi/abs/10.1111/j.2044-8295.1908.tb00182.x
Kitaoka, A. (2007). Tilt illusions after Oyama (1960): A review. Japanese Psychological Research, 49, 7-19.
https://onlinelibrary.wiley.com/doi/10.1111/j.1468-5884.2007.00328.x

Copyright Akiyoshi Kitaoka 2021 (February 24)
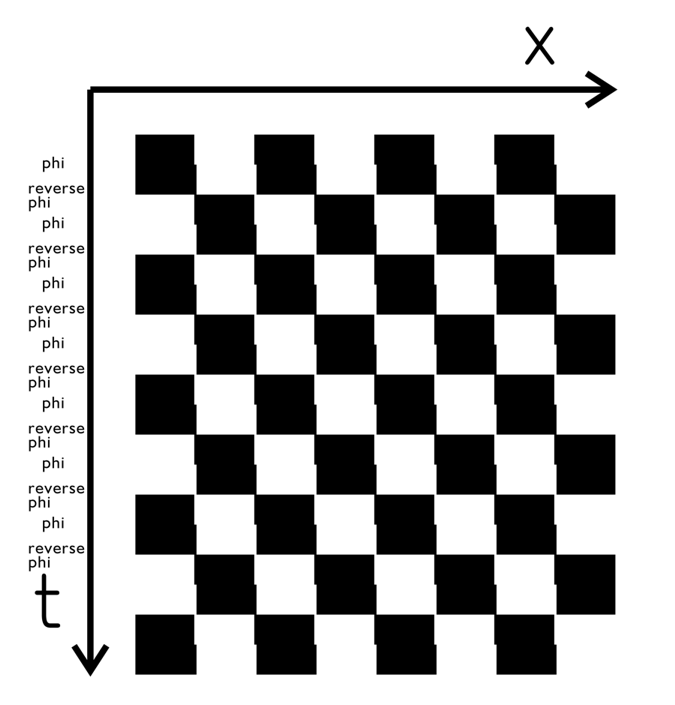
4ストローク運動とフレーザー錯視*との類似性
*この形態は「ずれたエッジの錯視」(illusion of shfted lines)(Kitaoka, 2007)(上図では、垂直に配列したずれたエッジの列が反時計回りに傾いて見える)である。

(100 ms / frame)

(30 ms / frame)
Copyright Akiyoshi Kitaoka 2021 (March 1)
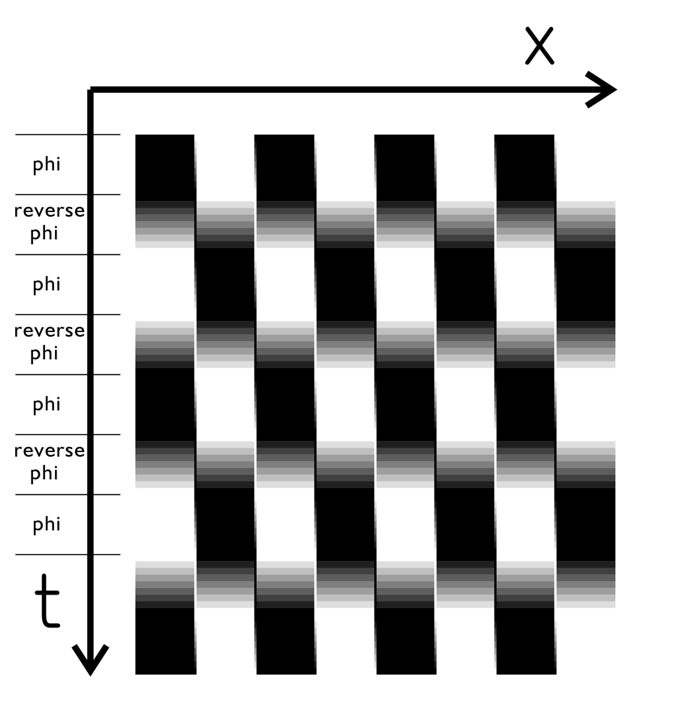
4ストローク運動とフレーザー錯視*との類似性(ファイは9フレーム、リバースファイも9フレーム)
*この形態は「ずれたエッジの錯視」(illusion of shfted lines)とモンタルボ錯視(Montalvo illusion)**(Lavatory Wall illusionともいう)の組み合わせ(上図では、垂直に配列した境界が反時計回りに傾いて見える)である。
**Kitaoka, A. (2007). Tilt illusions after Oyama (1960): A review. Japanese Psychological Research, 49, 7-19.
https://onlinelibrary.wiley.com/doi/10.1111/j.1468-5884.2007.00328.x

Copyright Akiyoshi Kitaoka 2021 (March 1)
<参考>
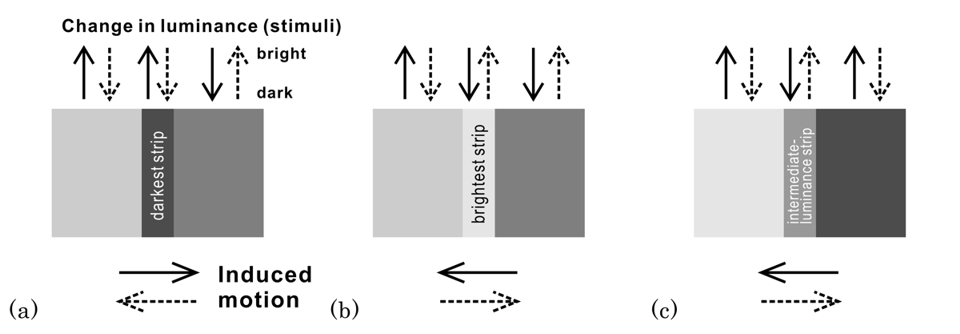
(a) and (b): reverse phi; (c) phi
Kitaoka, A. (2006). Configurational coincidence among six phenomena: A comment on van Lier and Csathó (2006). Perception, 35, 799-806. (Figure 6)
https://journals.sagepub.com/doi/10.1068/p5319b

境界の細線の輝度を変えることによる運動錯視と縞模様コードの錯視(Kitaoka, 1998)との類似性(全18フレーム)
Kitaoka, A. (1998). Apparent contraction of edge angles. Perception, 27, 1209-1219. https://journals.sagepub.com/doi/10.1068/p271209

(80 ms / frame)
Copyright Akiyoshi Kitaoka 2021 (March 1)

(30 ms / frame)
「運動視と傾き錯視が密接に関係する一連の静止画が動いて見える錯視があるが、それらの話題はまた別の機会に。」(北岡, 2021)


さて、ここで振り返ると、クラシックな傾き錯視の静止画が動いて見える錯視が比較的弱いことに気づく。

「ずれた線の錯視のドリフト錯視」
内側の領域が動いて見える。
Copyright Akiyoshi Kitaoka 2016 (September 1)

「フレーザー錯視のドリフト錯視」
内側の領域が動いて見える。
Copyright Akiyoshi Kitaoka 2016 (September 2)

「ずれたエッジの錯視のドリフト錯視」
内側の領域が動いて見える。
Copyright Akiyoshi Kitaoka 2016 (September 2)

「斜めのエッジの錯視のドリフト錯視」
内側の領域が動いて見える。
Copyright Akiyoshi Kitaoka 2016 (September 2)

カフェウォール市松模様錯視による動く錯視
内側の領域が動いて見える。垂直・水平の並びが傾いて見える。
Copyright Akiyoshi Kitaoka 2011 (February 1)

カフェウォール錯視による動く錯視
内側の領域が動いて見える。垂直の並びが傾いて見える。
Copyright Akiyoshi Kitaoka 2010 (April 2)
(この図形の被誘導線は貫通した灰色の線(モルタル線)ではないので、正確にはカフェウォール錯視ではない。なお、正しいカフェウォール錯視図形でも効果は同じ)

カフェウォール錯視による動く錯視
内側の領域が動いて見える。垂直の並びが傾いて見える。
Copyright Akiyoshi Kitaoka 2016 (May,2) (February 28, 2022)

カフェウォール錯視なくても動く錯視
Copyright Akiyoshi Kitaoka 2016 (May,2) (February 28, 2022)

カフェウォール錯視による動くハート
ハートの領域が動いて見える。垂直の並びが傾いて見える。
Copyright Akiyoshi Kitaoka 2022 (February 28)

"Café Wall wave"
Vertically and horizontally aligned gray lines appear to be wavy.
Copyright Akiyoshi Kitaoka 2011 (February 1)
"to move"
to slide or to wobble?

北岡明佳 (2012) 計算可能な錯視の探索的検討 (第4回錯覚ワークショップ 明治大学駿河台キャンパス アカデミーコモン9階 講義室309A・2012年3月14日(水)15:30-16:20) 発表に使用したウェブページ
「シマシマガクガク錯視」
Kitaoka, A. (2014). Visual illusion in ARTPOP and pop art. Japanese Journal of Psychonomic Science, 32(2), 232-234. PDF




オンオフさせると動いて見える。(2フレームで構成。1フレームは、150 ms)

オフの方が重要? (2フレームで構成。1フレームは、2000 ms)

傾き錯視はあるようなないようなドリフト錯視
内側の正方形領域が動いて見える。
Copyright Akiyoshi Kitaoka 2020 (June 6)

確認:線はなくても錯視的動きは見える。

確認:この方が錯視的動きは強い。

錯覚美術館に飾られていたトゲトゲドリフト錯視デザイン

錯覚美術館入り口(2011年6月5日)
結論
(というほど確かなもの・豊かなものではないが)
傾き錯視は静止画が動いて見える錯視と同時に存在することがよく見られるが、必ずしも同一のメカニズムによるものではない可能性がある。
 おしまい (The end)
おしまい (The end)
Thank you!
ご清聴ありがとうございました。

ツェルナー錯視、ミュンスターベルク錯視(カフェウォール錯視)、フレーザー錯視といった傾き錯視には、静止画が動いて見える錯視が同居している。このことには、筆者は比較的初期に気づき、そのデモをいくつか作成したが、先行研究にそのような記述があることを未だ知らない。筆者は2000年頃までには、市松模様の角に星や丸を置くことで傾き錯視と静止画が動いて見える錯視が同居する錯視画像の作成手法を確立した。その静止画が動いて見える錯視の格段の強さゆえ、その系統の錯視(四色錯視、トゲトゲドリフト錯視、エンボスドリフト錯視等)ばかり注目してきたが、「古典的な傾き錯視の画像に、そこまで強力な静止画が動いて見える錯視は観察できないのはなぜか」という問いを置き去りにしてきた。この点を問い直すことで、筆者がシマシマガクガク錯視と呼ぶ別系統の静止画が動いて見える錯視の関与が見えてくるようになった。

錯覚の解明・創作・応用への諸アプローチ
第16回錯覚ワークショップ
日時 : 2022年3月2日(水)、3日(木)
開催方法 :
オンライン開催(Zoom:Webinar機能利用)※事前申込制
組織委員長
杉原厚吉(明治大学)
組織委員
杉原厚吉(明治大学)、山口智彦(明治大学)、宮下芳明(明治大学)
北岡明佳(立命館大学)、一川誠(千葉大学)、星加民雄(東亜大学)、
近藤信太郎(岐阜大学)、森口昌樹(中央大学)、須志田隆道(サレジオ工業高等専門学校)
プログラム
3月2日(水)
13:00~13:40
星加民雄(東亜大学)
「坂道での速度抑制を目的とした錯視効果によるイメージハンプ施工に向けて」
13:40~14:20
西本博之(高知大学)
「錯視が解き明かす視覚の認知機能」
14:20~15:00
一川 誠(千葉大学)
「誘導運動と運動捕捉」
15:00~15:20
休憩
15:20~16:00
北岡明佳(立命館大学)
「傾き錯視と同居する静止画が動いて見える錯視の探求」
16:00~16:40
谷中一寿*(神奈川工科大学)、渡辺一樹(神奈川工科大学)
「クラウド錯視―主観的輪郭の回転で生ずる錯視」
3月3日(木)
10:00~10:40
杉原厚吉(明治大学)
「高さ反転錯視・起き上がり錯視・宙返り錯視
~共通の光学過程から生まれる3種類の知覚」
10:40~11:20
近藤信太郎(岐阜大学)、森将輝(慶應義塾大学)、須志田隆道*(サレジオ工業高等専門学校)
「網膜情報処理の数理モデルと視覚実験を用いたきらめき格子錯視の理解」
11:20~12:00
スリーピァン ピーラヤー*(芝浦工業大学)、山口泰(東京大学)
「双眼鏡錯視について」
12:00~13:30
休憩
13:30~14:10
間瀬実郎(呉工業高等専門学校)
「透視投影によるペンローズの階段のCGアニメーション」
14:10~14:50
日髙昇平*(北陸先端科学技術大学院大学)、金山春香 (北陸先端科学技術大学院大学)
「自由度を調整できる不可能立体の作図法」
14:50~15:10
休憩
15:10~15:50
大谷智子*(明治大学)、丸谷和史(NTT)、天内大樹(静岡文化芸術大学)
「ガラス建築に対する錯視の危険性の検討」
15:50~16:30
高橋康介*(立命館大学)、日髙昇平(北陸先端科学技術大学院大学)
「高次元空間構造の視覚的認識の可能性」
参考書

後藤倬男・田中平八(編)(2005) 錯視の科学ハンドブック 東京大学出版会

北岡明佳 (2010) 錯視入門 朝倉書店
