等分散性の検定では,分散の比でなく,Leveneの方法が用いられます。各クラスの平均値とローデータの値との差の絶対値を用いて,差の絶対値の平均がクラス間で異なるかどうかに関する検定(t 検定か分散分析)を行った結果が SPSSの表に F 値として示されています。
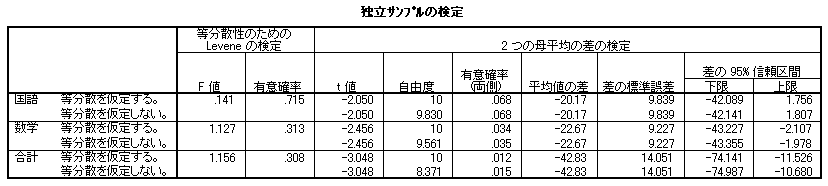
等分散が仮定されない場合,自由度を調整した検定(ウェルチの検定)を行うと説明されてきました。また,2つのサンプルが十分大きく,かつ同じ大きさであるならば,自由度の調整をしなくても大きな問題にならないと考えられてきました。しかし,最近は,等分散の仮定が成り立つか,成り立たないかに関わらずウェルチの検定を用いる方が良いとされています(Hayes & Cai, 2007)。ウェルチの検定では,自由度が少し小さくなりますが,検定を2回(等分散性の検定と t 検定)行うよりは良いだろうと考えられるからです。