平均値と定数の比較

平均値が計算されれば，母集団の平均に関する推定範囲が計算できます。推定範囲を利用すれば，平均値と特定の値との比較が可能です。

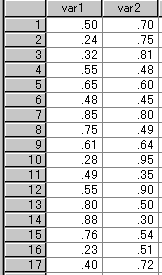
1. var1 と var2 の平均値と，定数 （例えば，0.5） との差が統計的に有意かどうかについて t 検定を行います。
   
   
   
   
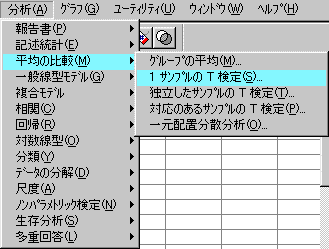
2. 分析から，1 サンプルの t 検定を選択します。
   
   
   
   
3. var1 と var2 を検定変数ボックスに移動させ，検定値を設定します。
   
   
   
   
4. OK ボタンを押すと，記述統計と検定結果が出力されます。
   
   
   
   

t 検定と効果の大きさ

• ｔ の値は，平均値の差と標準誤差から計算されます。上記の VAR1 では，
  
  0.0494 / 0.05134 = 0.962
  
  標準誤差は，標準偏差をサンプルの大きさの平方根で割った値です。
  
  
  
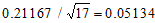
  データを加えても平均値の差と標準偏差が小さくならなければ， N が大きくなっただけ標準誤差は小さくなるので，小さな差であっても有意になる可能性が高くなります。しかし，データを加えることにより平均値の差が 0 に近づく可能性もあります。
  
  
• 平均値の差を，標準誤差でなく標準偏差で割った値 （d） は効果の大きさを表します。
  
  d = 0.0494 / 0.21167 = 0.2334
  
  d は比較的小さい値になりました。この値が正しいならば，差を有意にするためには多くのデータが必要になります。
  
  異なる研究結果を比較するときには，検定の結果 （例えば，ｔ の値） のみではなく，効果の大きさも含めて検討します。
  
  
• 効果が大きいということは，検証が容易であり，確かな傾向を発見したといえるでしょう。しかし，その明確な差異はありふれたことであるかもしれません。効果が小さいということは，不確かで検証が難しいことを意味します。小さな差異であっても，興味深い場合もあるでしょう。