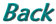モデルの適用

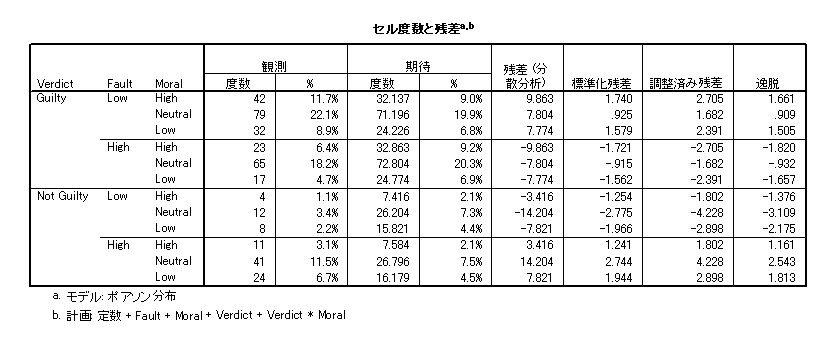
以下のようなクロス集計表 （Howell, 2002, p. 673） を考えてみます。Moral と Fault は犠牲者の特性です。一方，Verdict は被告に対する判決です。ですから，関心は犠牲者の特性と判決との間の関連性にあります。

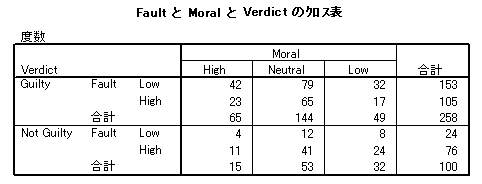
1. 集計結果を SPSS のデータシートに入力します。data をケースの重み付け変数として指定します。
   
   
   
   
2. メニューの分析から対数線型の一般的を選びます。
   
   
   
   
3. Verdict，Fault，Moral を因子欄に入れます。
   
   
   
   
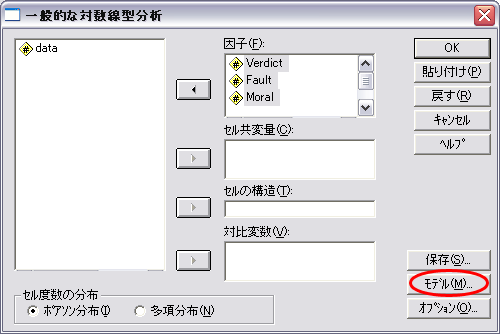
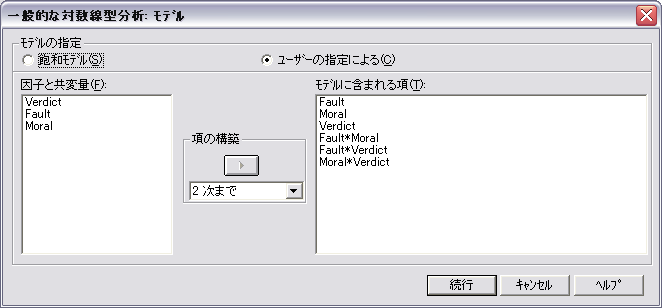
4. モデルをクリックして，「ユーザの指定による」 をチェックします。モデルの選択より，Fault × Verdictと Moral × Verdict を含むモデルが選択されました。Fault × Verdict と Moral × Verdict をモデルを含むように指定します。
   
   
   
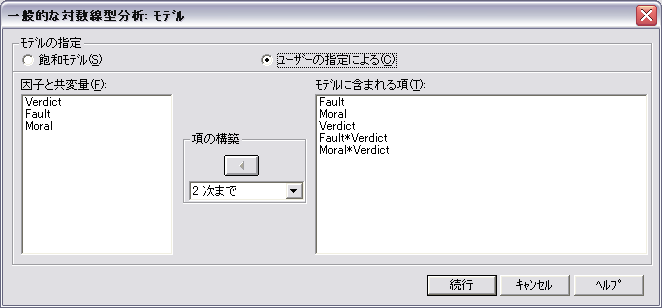
   階層的対数線型モデルなので，Fault，Verdict，Moral のそれぞれを明示的に含めても，含めなくても分析結果は変わりません。ただし，Fault，Verdict，Moral のそれぞれの効果を明示的に含ませるかどうかで，パラメータの推定値が異なります。パラメータはオプションで指定すれば出力されます。
   
   
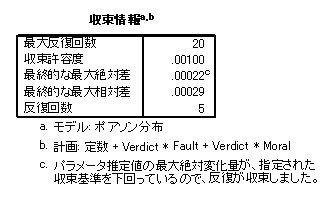
5. OKをクリックすると出力が表示されます。収束情報から，無事に収束していることがわかります。収束しない場合には，オプションの最大反復回数を大きな値に変更してください。
   
   
   
   
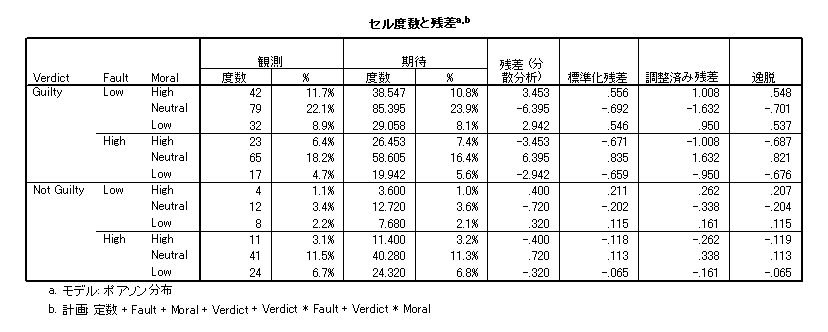
6. 適合度検定の結果が有意でないことは，モデルが良く当てはまっていることを示します。
   
   
   
   
7. 期待度数と残差が表示されます。調整済み残差を使って ｚ 検定を行うことができます。
   
   
8. 今度は，Fault × Verdict をモデルに含めない場合を考えてみましょう。
   
   
   
   
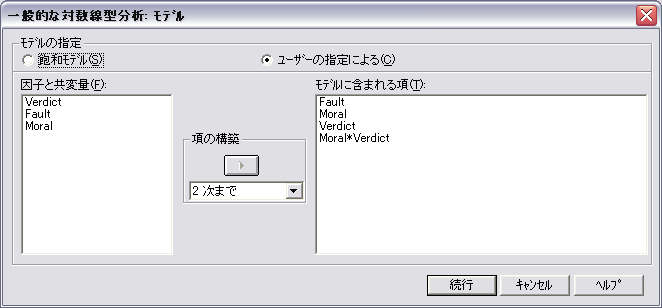
9. 適合度検定が有意になりました。モデルはデータに適合しないことを示しています。
   
   
   
   Fault × Verdict をモデルから除いたことによるカイ二乗値の増加分は 40.163 - 2.812 = 37.351 になります。その自由度も差をとり 5 - 4 = １ になります。χ2(1) = 37.351 が Fault × Verdict と Moral × Verdict を含むモデルにおける Fault × Verdict の貢献度になります。
   
   
10. 調整済み残差は z 値とみなすことができるので，調整済み残差の絶対値が 1.96 より大きいセルは当てはまりが悪いといえます。
    

モデルに含まれる項を変えて，適合度を比較してみます。

1. 2変数の交互作用をすべて含むモデル （Fault × Moral × Verdict を除いたモデル） を当てはめてみます。
   
   
   
   
   
   
2. 次に，上記のモデルから Fault × Verdict を除外した場合を考えてみましょう。
   
   
   
   
   
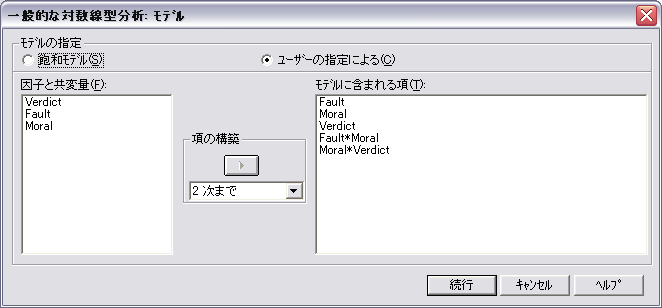
   モデルから Fault × Verdict を除去したことによるカイ二乗値の増加分は 37.245 - .255 = 36.99 になります。この値は，Fault × Verdict と Moral × Verdict を含むモデルから Fault × Verdict を除去した場合の値とはいくらか異なります。