対応のあるデータのクロス集計
例題: 説明前後の態度の変化を調べました。
- 50名の態度変化は,以下のようなものでした。説明の影響を知るために,賛成から反対に移った人数 (5名) と,反対から賛成に移った人数 (17名) に違いがあるかどうかを検討します。態度を変えなかった 28名については分析から除外します。
| 説明前 |
説明後 |
計 |
| 賛成 |
反対 |
| 賛成 |
15 |
5 |
20 |
| 反対 |
17 |
13 |
30 |
| 計 |
32 |
18 |
50 |
|
賛成する比率が説明前後で変化しないことが帰無仮説になります。各セルの頻度を f11, f12, f21 とすると,(f11+f12)-(f11+f21) = f12-f21 であるので,説明前後で比率が変わらないことは f12 と f21 が等しことを意味します (詳しくは,Agresti, 2003, 9章)。
- 集計結果を SPSS のデータシートに入力します。

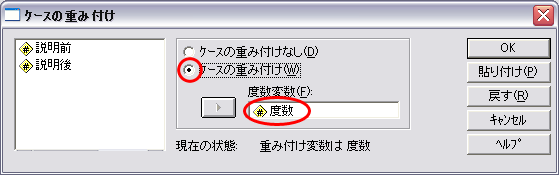
- 度数をケースの重み付け変数として指定します。

- 左の枠内にあった度数を選択し,度数変数の欄に挿入します。
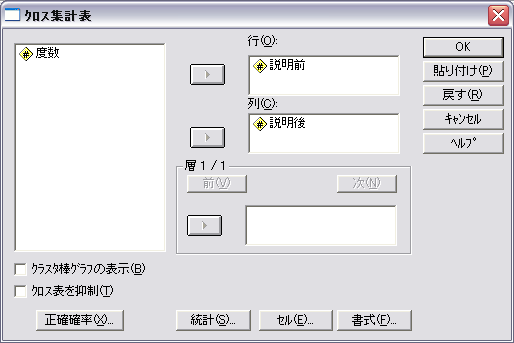
- 分析メニューの記述統計からクロス集計表を選択します。

- 説明前を行の欄に,説明後を列の欄に入力します。
- セルを選択し,パーセンテージを表示するように設定します。
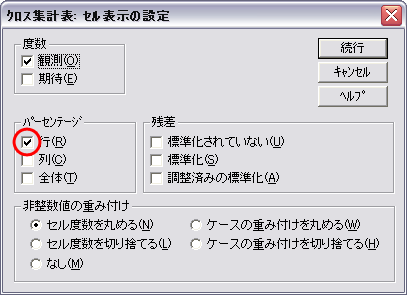
- 統計の設定では,McNemar をチェックします。クロス集計の非対角セルの対称性を検定することができます。
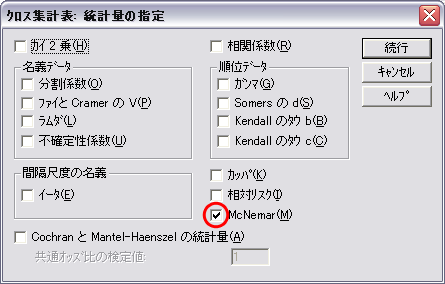
- カイ二乗検定の出力が表示されますが,実際には二項分布の確率が計算されます。
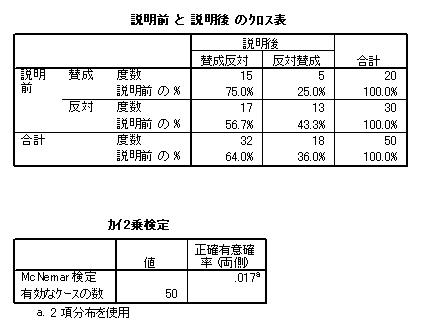
上記の McNemar検定は,SPSS を用いて 2項分布の確率を計算した結果と同じです。そのことを確かめてみましょう。
- 賛成から反対に移った 5名と,反対から賛成に移った 17名を SPSS のデータシートに入力します。

- 左の枠内にあった頻度を選択し,度数変数の欄に挿入します。

- 分析メニューのノンパラメトリック検定から 2項を選択します。

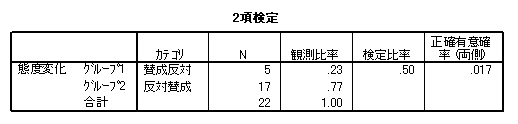
- 検定変数リストに態度変化を加えます。また,検定比率は .50 です。
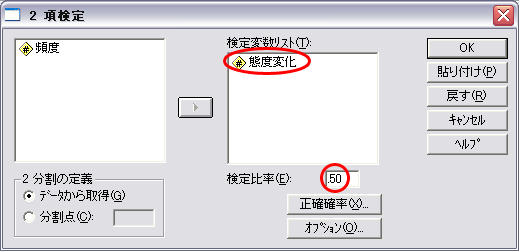
- 2項検定の結果は以下のようになります。McNemar検定と同じ確率が表示されました。