立命館大学総合心理学部
Stan は,乱数を用いて,モデルのパラメータに関する確率的分布を推測します。乱数を用いた数値計算の手法はモンテカルロ法と呼ばれ,統計学や数値解析など広く利用されています。乱数を用いた計算では生成された乱数に計算結果が依存しますから,安定した結果を効率的に算出する方法の開発が大きな課題になります。補助的な変数を導入して乱数が重要な範囲に集中するようにしたり,アルゴリズムを工夫して無駄な乱数の生成を制限すようにして,効率的で,再現性の高い乱数生成の手法が工夫されています。
ここでは,Stan を使って,心理学の実験結果,具体的には条件別の平均値を比較する方法を検討します。Stanは,心理学的モデルあるいは認知モデルのパラメータ推測においても利用されていますが,ここでは実験で得られた条件別平均の母平均を推測する方法を検討しています。
Stan はデータから母平均の事後確率分布(以後,事後分布)を推測します。母平均の事前確率分布(以後,事前分布)とデータから,1つの母平均ではなく,母平均の確率分布を推測するところがベイズ統計です。ベイズ統計ではベイズ因子(Bayes factor)を用いた方法も広く用いられていますが(たとえば,Morey, n.d.; Rouder et al., 2016),ここではパラメータの事後分布を求めて分析する方法(たとえば,Kruschke, 2015; Tendeiro & Kiers, 2019; 豊田, 2017)を検討します。
実験参加者間要因と実験参加者内要因を組み合わせた混合計画は心理学実験でしばしば用いられます。Howell(2013, p. 468)の Table 14.4 には,薬物(midazolam)の影響について調べるために,midazolam の投与後,ラットの活動性を 5分ごとに6回測定し,3条件で比較した実験(D. A. King による博士論文, 1986)の結果が示されています。この実験は,midazolam へのラットの耐性が条件づけに基づくのかどうかを検討するために行われました(関連する研究として,King,Bouton,& Musty,1987)。
活動性の計測を行うテストの前にラットに何度か注射し,midazolam か生理食塩水を投与します。第1の条件は統制条件で,テスト前に生理食塩水を注射され,テストで初めて midazolam が投与されました。第2の条件は同環境条件で,テスト前とテストでの薬物投与を同じ環境で行いました。統制条件でも注射を行う環境は変化していませんでしたが,第3の条件である異環境条件では異なっていました。すなわち,テスト前に行われた midazolam の投与はテストと異なる環境で行われています。
統制条件は midazolam の影響で活動性が低下しますが,代謝によって徐々に回復すると予想できます。同環境条件ではテスト前の投与によって,midazolam への耐性をラットが獲得するため,活動性の低下が抑えられると予想できます。テスト前に獲得した耐性が条件づけに基づいているのならば,異環境条件では注射を行う環境が変わることによって耐性(条件反応)が失われると予想されました。
6回の繰り返しを 3条件で比較していますので,18個の異なる平均があります。このデータを R(4.0.4) と RStan(2.21.2)を使って分析してみました。
# データ,Howell, 2002, pp. 480-483 #
x11<-c(150, 335, 149, 159, 159, 292, 297, 170)
x12<-c(44, 270, 52, 31, 0, 125, 187, 37)
x13<-c(71, 156, 91, 127, 35, 184, 66, 42)
x14<-c(59, 160, 115, 212, 75, 246, 96, 66)
x15<-c(132, 118, 43, 71, 71, 225, 209, 114)
x16<-c(74, 230, 154, 224, 34, 170, 74, 81)
x21<-c(346, 426, 359, 272, 200, 366, 371, 497)
x22<-c(175, 329, 238, 60, 271, 291, 364, 402)
x23<-c(177, 236, 183, 82, 263, 263, 270, 294)
x24<-c(192, 76, 123, 85, 216, 144, 308, 216)
x25<-c(239, 102, 183, 101, 241, 220, 219, 284)
x26<-c(140, 232, 30, 98, 227, 180, 267, 255)
x31<-c(282, 317, 362, 338, 263, 138, 329, 292)
x32<-c(186, 31, 104, 132, 94, 38, 62, 139)
x33<-c(225, 85, 144, 91, 141, 16, 62, 104)
x34<-c(134, 120, 114, 77, 142, 95, 6, 184)
x35<-c(189, 131, 115, 108, 120, 39, 93, 193)
x36<-c(169, 205, 127, 169, 195, 55, 67, 122)
x1<-cbind(x11, x12, x13, x14, x15, x16)
x2<-cbind(x21, x22, x23, x24, x25, x26)
x3<-cbind(x31, x32, x33, x34, x35, x36)
m1<-apply(x1, 2, mean)
m2<-apply(x2, 2, mean)
m3<-apply(x3, 2, mean)
ms<-cbind(m1, m2, m3)
matplot(ms, type="b", pch="CSD", col=2:4, cex=1, lwd=1.5, lty=1, xlab="Interval", ylab="Activity", bty="l")
legend(4.5, 350, pch="CSD", c("Control","Same","Different"), col=2:4, cex=1, lwd=1.5, lty=0, bty="n")平均値の計算と作図を行う R のコードです。
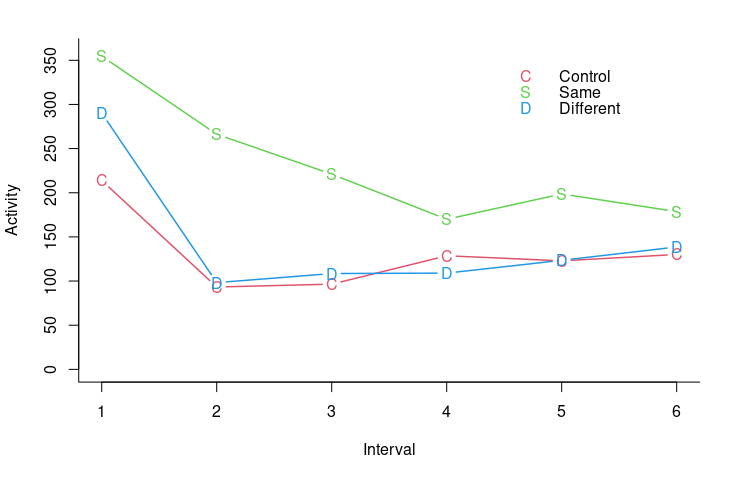
図の縦軸は各条件の平均値、横軸は6回の繰り返し測定を示します。実験ではラットが使われましたが,ここでは繰り返し測定を実験参加者内要因,3つの異なる測定条件を実験参加者間要因と記述します。実験参加者間要因を要因A,実験参加者内要因を要因B とします。
A=1
213.88 93.25 96.50 128.62 122.88 130.12
79.21 93.27 54.10 70.31 65.24 74.55
A=2
354.62 266.25 221.00 170.00 198.62 178.62
89.91 109.69 69.88 78.11 66.22 83.59
A=3
290.12 98.25 108.50 109.00 123.50 138.62
69.32 53.48 62.66 52.53 50.10 56.02
各条件の平均値と標準偏差(不偏分散の平方根)です。
ここでは各条件の平均を,全体の平均,要因A の効果,要因B の効果,2つの要因の交互作用効果に分けて推測する Stan のモデルを検討します。すなわち,要因A における各水準の効果(3-1個のパラメータ),要因B の各水準の効果(6-1個のパラメータ),交互作用に効果((3-1)x(6-1)個のパラメータ),そして,全体の平均の計18個のパラメータを推測します。このパラメータ数は,当然ですが,平均の数に一致します。平均についてのパラメータに加えて,1つの分散と 1つの相関を推測します。繰り返し測定されたデータ間には相関があります。
data {
int<lower=0> N; // No. of Data
int<lower=0> a; // No. of factor A levels
int<lower=0> b; // No. of factor B levels
vector[b] x[N]; // Data
int<lower=0> A[N]; // levels of factor A
real mL;
real mH;
real vL;
real vH;
}
parameters {
real<lower=mL, upper=mH> muT; // total mean
real muA[a-1]; // factor A
vector[b-1] muB; // factor B
vector[b-1] muAB[a-1]; // interaction between A and B
real<lower=vL, upper=vH> vE; // variance
real<lower=-1, upper=1> rho; // correlation
}モデルの data部分では,実験参加者の数(N),各要因の水準数(a,b),平均の最小値と最大値(mL と mH),分散の最小値と最大値(vL と vH)などを定義します。最小値と最大値は平均と分散の事前分布を定義します。整数の配列A には要因A の水準を示す数字が代入されます。要因Aの水準1,2,3 は,それぞれ,統制条件,同環境条件,異環境条件です。
parameters部分では推測するパラメータを定義します。要因A の効果を表す muA は a-1個の要素を持つ配列,要因B の効果を表す muB は b-1個の要素を持つベクトルとして定義しています。交互作用を表す muAB はベクトルの配列とします。全体の平均(muT)と分散(vE),相関(rho)は,それぞれ,実数で定義しています。
transformed parameters {
real mA[a];
vector[b] mB;
vector[b] mAB[a];
cov_matrix[b] Sigma;
for (i in 1:(a-1)) {
mA[i] = muA[i];
}
mA[a] = -1*sum(muA);
for (j in 1:(b-1)) {
mB[j] = muB[j];
}
mB[b] = -1.0*sum(muB);
// AB
for (i in 1:(a-1)) {
for (j in 1:(b-1)) {
mAB[i, j] = muAB[i, j];
}
mAB[i, b] = -1.0*sum(muAB[i]);
}
for (j in 1:b) {
real temp = 0.0;
for (i in 1:(a-1)) {
temp += mAB[i, j];
}
mAB[a, j] = -1.0*temp;
}
// Sigma
for (i in 1:(b-1)) {
for (j in (i+1):b) {
Sigma[i, j] = vE*rho;
}
}
for (i in 1:b) {
Sigma[i, i] = vE;
}
for (i in 2:b) {
for (j in 1:(i-1)) {
Sigma[i, j] = Sigma[j, i];
}
}
}
model {
muA ~ normal(0, sqrt(vH));
muB ~ normal(0, sqrt(vH));
for (i in 1:(a-1)) {
muAB[i] ~ normal(0, sqrt(vH));
}
for (i in 1:N) {
x[i] ~ multi_normal(muT+Ma[A[i]]+Mb+Mab[A[i]], Sigma);
}
}transformed parameters では,まず,各要因の効果と関連する制約を定義するために,muA を mA に,muB を mBに,muAB を mAB に,それぞれ,変換しています。muA は a-1個の要素を持っていますが,mA は a個の要素を持っています。a-1個については muA を mA に代入するのみですが,a番目の mA についてはmuA の合計に -1 を掛けた値を代入しています。つまり,mA の各要素の合計は 0 になります。muB と mB についても同じです。交互作用については,少し複雑になりますが,考え方は同じです。交互作用の各効果は行で合計しても,列で合計しても 0 になります。Stan は収束する乱数を生成する過程でこれらの制約を満たすようにします。
Sigma は6×6の共分散行列です。共分散は vE と rho の積です。対角要素には分散(vE)が代入されます。検討しているモデルでは,どの条件でも誤差の分散が同じ大きさであり,条件間の相関が同じであると仮定しています。
model の部分には,まず,muA,muB,muAB の事前分布が記述されています。これらのパラメータは要因の効果を示していますから,0 を中心に分布すると考えられますので,平均が 0 の正規分布を事前分布とするのは自然でしょう。正規分布の標準偏差は,分散の事前分布を定義するときに用いた vH を用いています。事前分布の標準偏差に定数を用いず,ガンマ分布などを用いれば階層的ベイズモデルになります。階層的なモデルは推定値が控えめになる(全体の平均に近づく)ので,事後分布を用いて効果の大きさについて検討したり,条件間の比較を行うときには,階層的なモデルが望ましいとされています(Gelman, Hill, & Yajima, 2012; Kruschke, 2015)。
次に,データ(x)とパラメータの関係を多変量正規分布を用いて記述しています。被験者内要因B の水準数と同じ数の母平均が多変量正規分布すると仮定しています。multi_normal では,muT と Ma,Mb,Mab を加算して平均を算出しています。muTは実数,Ma は配列,Mb はベクトル,Mab はマトリックスですが,Stan はこれらを混合して計算できます。
generated quantities {
vector[b] mu[a];
matrix[a, b] Mab;
real vA;
real vB;
real vAB;
real sigmaE = sqrt(vE);
// eata squired
real eA;
real eB;
real eAB;
// partial eata squired
real eAp;
real eBp;
real eABp;
real log_lik[N];
for (i in 1:a) {
mu[i] = muT+mA[i]+mB+mAB[i];
}
for (i in 1:N) {
log_lik[i] = multi_normal_lpdf(x[i] | muT+mA[A[i]]+mB+mAB[A[i]], Sigma);
}
}generated quatities の部分では,各条件の平均値を合成し,mA,mB,mAB の分散を計算しています。log_lik は確率密度の対数です。モデルの予測誤差を表す情報量基準(WAIC;渡辺,n.d.; 豊田,2017)を計算するために用います。
> library(loo)
> print(waic(log_lik))
Computed from 20000 by 24 log-likelihood matrix
Estimate SE
elpd_waic -807.3 9.3
p_waic 18.4 2.2
waic 1614.5 18.5
18 (75.0%) p_waic estimates greater than 0.4. We recommend trying loo instead.
> print(loo(fit))
Computed from 20000 by 24 log-likelihood matrix
Estimate SE
elpd_loo -807.7 9.3
p_loo 18.8 2.3
looic 1615.3 18.7
------
Monte Carlo SE of elpd_loo is 0.1.
Pareto k diagnostic values:
Count Pct. Min. n_eff
(-Inf, 0.5] (good) 20 83.3% 2657
(0.5, 0.7] (ok) 4 16.7% 1194
(0.7, 1] (bad) 0 0.0% <NA>
(1, Inf) (very bad) 0 0.0% <NA>
All Pareto k estimates are ok (k < 0.7).
See help('pareto-k-diagnostic') for details.loo パッケージを使って WAIC の計算しています。fit には Stan による分析結果が代入されています。ただし,モデルでは多変量正規分布を仮定していますので,被験者内要因Bについては multi_normal_lpdf() によって 1つの値にまとめられています。そのため,分析に投入したデータの値の数は 3(要因A)x 6(要因B)x 8(ラット)の144個ですが,3 x 1 x 8 = 24個の確率密度の値から WAIC の値が計算されています。
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 5% 50% 95% 97.5% n_eff Rhat
mu[1,1] 213.93 0.16 26.97 160.56 169.71 214.08 258.07 266.48 28667 1
mu[1,2] 93.70 0.16 27.01 40.81 49.24 93.53 137.97 147.22 28170 1
mu[1,3] 96.78 0.16 26.89 43.10 51.99 97.25 140.58 149.08 28624 1
mu[1,4] 128.82 0.16 26.66 76.43 85.28 128.58 172.49 181.23 29554 1
mu[1,5] 123.02 0.15 26.60 70.23 79.35 123.41 166.08 175.30 29498 1
mu[1,6] 130.48 0.16 26.91 78.14 86.43 130.41 174.68 184.03 26928 1
mu[2,1] 354.45 0.16 27.15 300.97 310.00 354.46 398.75 407.76 28101 1
mu[2,2] 266.09 0.16 27.04 212.37 221.36 266.26 310.49 318.90 28841 1
mu[2,3] 220.82 0.16 26.80 167.19 176.45 220.96 264.32 272.77 28777 1
mu[2,4] 169.94 0.16 27.00 116.56 125.60 169.94 214.12 222.71 27806 1
mu[2,5] 198.55 0.16 26.98 145.16 154.12 198.58 242.61 251.64 27723 1
mu[2,6] 178.37 0.17 27.05 125.23 133.93 178.50 222.78 231.57 24946 1
mu[3,1] 289.94 0.15 26.76 237.01 245.80 289.97 334.23 343.00 33921 1
mu[3,2] 98.29 0.15 26.66 46.12 54.08 98.50 141.74 150.31 31813 1
mu[3,3] 108.49 0.15 26.92 55.83 64.21 108.74 152.99 161.46 33355 1
mu[3,4] 109.00 0.15 26.67 56.64 65.21 109.13 152.88 161.80 32689 1
mu[3,5] 123.38 0.15 26.78 70.46 79.34 123.54 167.82 176.62 33315 1
mu[3,6] 138.51 0.16 26.69 86.23 94.75 138.53 182.08 190.48 26576 1
sigma 75.76 0.06 7.82 63.23 64.83 74.79 90.03 93.83 15183 1
rho 0.51 0.00 0.10 0.32 0.35 0.51 0.67 0.70 18298 1平均の事前分布を 0 から 1,000 の一様分布,分散の事前分布を 0 から 100,000 までの一様分布として計算した結果です。mu は各条件の平均に関するパラメータ(すなわち母平均),sigmaE は各条件の標準偏差に関するパラメータ,rho は条件間の相関に関するパラメータです。
このモデルから計算された WAIC の値は 1614.5 になりました。
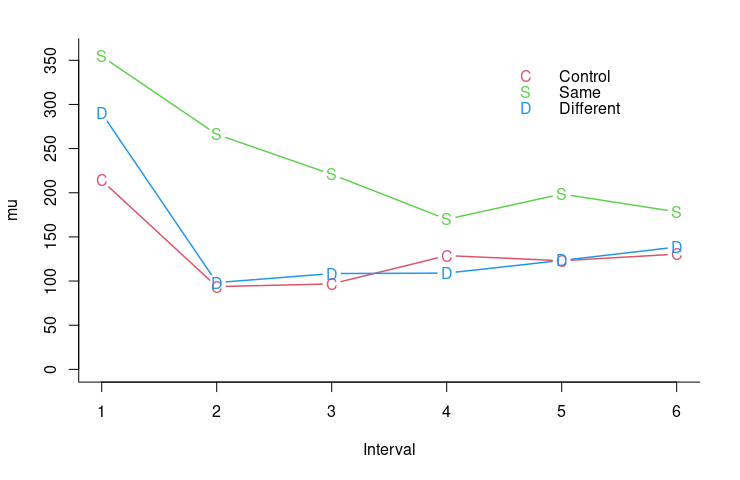
推測された母平均の事後期待値(平均)をプロットしてみると,データの平均によく一致していることが分かります。
mean se_mean sd 2.5% 5% 50% 95% 97.5% n_eff Rhat
muT 169.03 0.07 12.12 144.55 148.99 169.14 188.79 193.17 33440 1
mA[1] -37.91 0.11 16.99 -71.56 -65.84 -37.81 -10.21 -4.53 25537 1
mA[2] 62.34 0.10 17.05 28.73 34.35 62.23 90.49 96.09 27176 1
mA[3] -24.43 0.10 16.93 -57.82 -52.07 -24.46 3.26 9.09 29572 1
mB[1] 117.08 0.05 9.85 97.61 101.09 117.04 133.12 136.61 33037 1
mB[2] -16.34 0.06 9.74 -35.40 -32.19 -16.35 -0.34 2.68 30049 1
mB[3] -27.00 0.05 9.72 -46.14 -42.91 -27.09 -10.79 -7.68 34858 1
mB[4] -33.11 0.05 9.74 -52.24 -49.19 -33.06 -17.14 -13.93 34282 1
mB[5] -20.71 0.05 9.69 -39.74 -36.68 -20.67 -5.01 -1.76 36017 1
mB[6] -19.91 0.07 9.80 -39.15 -36.08 -19.90 -3.72 -0.59 21660 1
mAB[1,1] -34.27 0.08 13.72 -60.91 -56.92 -34.20 -11.66 -7.25 27223 1
mAB[1,2] -21.09 0.09 13.81 -48.31 -43.81 -21.00 1.69 5.87 26171 1
mAB[1,3] -7.34 0.08 13.93 -34.84 -30.29 -7.30 15.69 19.93 26908 1
mAB[1,4] 30.81 0.08 13.71 4.15 8.50 30.90 53.28 58.19 26038 1
mAB[1,5] 12.61 0.09 13.80 -14.51 -10.01 12.55 35.08 39.57 26216 1
mAB[1,6] 19.27 0.09 13.86 -7.97 -3.41 19.23 42.05 46.53 23671 1
mAB[2,1] 6.00 0.08 13.73 -20.79 -16.53 5.96 28.45 33.01 27342 1
mAB[2,2] 51.06 0.09 13.88 23.68 27.97 51.02 74.03 78.37 26559 1
mAB[2,3] 16.45 0.08 13.77 -11.14 -6.44 16.45 39.05 43.44 26981 1
mAB[2,4] -28.32 0.09 13.71 -55.11 -50.75 -28.32 -5.67 -1.51 25840 1
mAB[2,5] -12.11 0.09 13.80 -39.25 -34.79 -12.12 10.57 14.95 25891 1
mAB[2,6] -33.09 0.09 13.69 -59.95 -55.49 -33.04 -10.71 -6.31 22752 1
mAB[3,1] 28.27 0.07 13.84 1.05 5.59 28.38 51.22 55.57 41358 1
mAB[3,2] -29.97 0.07 13.85 -56.98 -52.70 -29.94 -7.10 -3.05 38316 1
mAB[3,3] -9.11 0.07 14.10 -36.68 -32.28 -9.08 14.04 18.58 41361 1
mAB[3,4] -2.49 0.07 13.79 -29.86 -25.05 -2.48 20.31 24.92 40425 1
mAB[3,5] -0.51 0.07 13.88 -27.91 -23.21 -0.53 22.34 26.67 39328 1
mAB[3,6] 13.82 0.09 13.79 -13.28 -9.04 13.75 36.60 40.60 21187 1定義されたパラメータの推測値です。muT は全体の平均,mA は要因A の効果,mB は要因B の効果,mABはそれらの交互作用の効果を示しています。たとえば,mu[1, 1] = muT + mA[1] + mB[1] + mAB[1, 1] になります。
mA,mB,mAB についての確信区間が示されていますので,たとえば,mA[2] の値はかなり高く,95%確信区間は 28~96 であり,0 を含まないことが分かります。要因B の効果でも,交互作用の効果でも,95%確信区間に 0 を含まない要素があります。これらの値はデータの単位(任意の単位であっても)を保存していますので,効果の大きさをデータに即して考えることができます。
分散分析で用いられる帰無仮説は,ある要因のすべての水準の平均が等しいとする仮説ですから,全体平均のみを仮定する Stan のモデルは帰無仮説に相当するといえます。要因A と 要因B,交互作用を仮定せずに(それらの効果を 0 として)全体平均のみを推測すると(すなわち,平均が1つ,分散が1つ,相関が1つの,計3つのパラメータを推測するモデルでは),WAIC の値は 1711.1 になり,あてはまりが良いとはいえません。要因A のみを仮定し,要因B と交互作用の効果を考えないモデルでは,WAIC の値が 1702.2 になります。要因B のみを仮定するモデルでは,WAIC の値が 1632.5 です。要因A と要因B の効果を仮定し,交互作用の効果を仮定しないモデルでは,WAIC の値は 1623.6 ですので,交互作用を含めたモデルで WAIC の値が最も小さいくなることが分かります。
mA,mB,mAB の確信区間の分析でも,WAIC を用いた分析でも,要因A と 要因B,交互作用を含めたモデルが妥当だといえます。
平均に関するパラメータは全部で18個ですが,パラメータの数を減少させることができそうです。研究者が前もって検討した仮説に基づいてパラメータの選択を行うことができればその方が望ましいのですが,ここではデータに基づいて事後的にパラメータの選択を行います。
要因A と要因B,それらの交互作用についてデータの平均を使って確認してみます。
> mt<-mean(ms)
> ma<-apply(ms, 2, mean)-mt
> round(ma, 2)
m1 m2 m3
-38.15 62.50 -24.35
> mb<-apply(ms, 1, mean)-mt
> round(mb, 2)
x11 x12 x13 x14 x15 x16
117.19 -16.44 -27.02 -33.15 -20.69 -19.90
> mab<-ms-matrix(ma, 6, 3, byrow=T)-mb-mtms には各条件の平均値が代入されています。ma と mb の値にそれぞれ要因A と要因B の効果が代入されています。mab は交互作用を示します。ma,mb,mab の合計は,それぞれ,0 になります。
ma の値を見ると,要因A については水準2(同環境条件) の平均が高く,水準1 と 3(統制条件と異環境条件)はほぼ同じと考えることができそうです。mb を見ると,要因B については水準1 の平均が高く,その他はほぼ同じといえるでしょう。mab は以下のようになりました。(行列を転置しています。)
| mab | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1: Control | -34.19 | -21.19 | -7.35 | 30.90 | 12.69 | 19.15 |
| 2: Same | 5.92 | 51.17 | 16.50 | -28.38 | -12.21 | -33.00 |
| 3: Different | 28.27 | -29.98 | -9.15 | -2.52 | -0.48 | 13.85 |
統制群と異環境条件では,早い段階で活動性が弱まり,その後,活動性が高くなっていきます。同環境条件では 1 から 3 の区間では活動性が高く,その後に活動性が下がっていますので,統制群・異環境条件とは異なるパターンを示しています。mab を大きさの順に並べて検討してみます。
> table(sort(round(mab, -1)))
-30 -20 -10 0 10 20 30 50
4 1 3 2 3 2 2 1mab の値を丸めて大きさの順に並べ,度数を表示させています。-30~-20,-10~10,20~30,50 の4つの範囲に分け,交互作用に関する 4つのパラメータ(muAB1~muAB4)を仮定すればよさそうです。
交互作用の場合,行の合計と列の合計がともに 0 になる必要があります。10個(5×2)のパラメータが必要なところを 4つに減らしているので,そのような制約を計算する方法は幾通りもあり,計算方法によって推測されるパラメータの値が異なる結果になります。
どの行あるいは列を,他の行あるいは他の列の合計に -1 をかけた値にするかするかを決めることにします。
> round(apply(mab, 2, sd), 2)
m1 m2 m3
25.12 31.52 19.90
> round(apply(mab, 1, sd), 2)
x11 x12 x13 x14 x15 x16
31.65 44.53 14.32 29.72 12.45 28.70mab の変動は,要因A の水準3 が最も小さいことが,要因B については水準5 の変動が最も小さいことが分かります。要因A については水準3,要因B の水準5 を,それぞれ,制約を計算する起点にします。すなわち,mAB[3, 1] = -1*(mAB[1, 1]+mAB[2. 1]) とします。同時に,mAB[1, 5] = -1*(mAB[1, 1]+mAB[1, 2]+mAB[1, 3]+mAB[1, 3]+mAB[1, 6])とします。他の要素についても同様です。どの列についても 5行目を,どの行についても 3行目を制約の起点とします。
| mAB | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1: Control | muAB 1 | muAB 1 | muAB 2 | muAB 3 | muAB 3 | |
| 2: Same | muAB 2 | muAB 4 | muAB 3 | muAB 1 | muAB 1 | |
| 3: Different |
交互作用の大きさに応じて muAB1~muAB4 を割り当てると,muAB1~muAB4が表の青色部分に含まれていることを確認します。黄色い部分には青い部分の和と釣り合う大きさが計算され割り当てられます。
検討する Stan のモデルでは,全体の平均について 1つのパラメータ,要因A と要因B のそれぞれについて1つのパラメータ,交互作用について 4つのパラメータ,そして,相関と分散について 1つずつのパラメータ,合計9つのパラメータを仮定します。モデルの parametes部分と transformed parameters の一部を以下に示します。
parameters {
real<lower=mL, upper=mH> muT; // 全体平均
real muA1;
real muB1;
real muAB[4];
real<lower=vL, upper=vH> vE; // 分散
real<lower=-1, upper=1> rho; // 相関
}
transformed parameters {
real mA[a];
vector[b] mB;
vector[b] mAB[a];
cov_matrix[b] Sigma;
mA[1] = (-1.0/2.0)*muA1;
mA[2] = muA1;
mA[3] = (-1.0/2.0)*muA1;
mB[1] = muB1;
mB[2] = (-1.0/5.0)*muB1;
mB[3] = (-1.0/5.0)*muB1;
mB[4] = (-1.0/5.0)*muB1;
mB[5] = (-1.0/5.0)*muB1;
mB[6] = (-1.0/5.0)*muB1;
// AxB interaction
mAB[1, 1] = muAB[1];
mAB[1, 2] = muAB[1];
mAB[1, 3] = muAB[2];
mAB[1, 4] = muAB[3];
mAB[1, 6] = muAB[3];
mAB[2, 1] = muAB[2];
mAB[2, 2] = muAB[4];
mAB[2, 3] = muAB[3];
mAB[2, 4] = muAB[1];
mAB[2, 6] = muAB[1];
{
real tempA[a-1];
for (i in 1:(a-1)) {
tempA[i] = 0.0;
for (j in 1:b) {
if (j == 5) continue;
tempA[i] += mAB[i, j];
}
mAB[i, 5] = -1.0*tempA[i];
}
mAB[a, 5] = sum(tempA);
for (j in 1:b) {
if (b == 5) continue;
mAB[3, j] = -1.0*(mAB[1, j]+mAB[2, j]);
}
}計算を行うと,WAIC の値は 1596.7 になりました。18個の母平均を推測するよりも,7つ(全体の平均が1つ,要因Aが1つ,要因Bが1つ,交互作用が4つ)の母平均を推測するモデルの方が当てはまりが良い結果になりました。
条件によって平均が変動するように,条件間の相関も変動する可能性があります。繰り返し測定は 6回ですから,それらの間の相関は 6x(6-1)/2 = 15 です。3条件で繰り返し測定を行っていますので,15x3 = 45 個の相関をパラメータとする Stan のモデルによる分析を行いました。7+45個のパラメータを推測した結果,WAIC の値は 1590.4 になりました。45-1個のパラメータを追加したにもかかわらず,WAIC の値の小さくなっています。相関の違いはデータの予測にとって重要なのかもしれません。
交互作用の分析と同様に,相関の大きさを整理して比較してみます。
A=1
0.938 (1 2) 0.586 (1 3) 0.428 (1 4) 0.697 (1 5) 0.36 (1 6)
0.533 (2 3) 0.295 (2 4) 0.513 (2 5) 0.438 (2 6)
0.910 (3 4) 0.337 (3 5) 0.846 (3 6)
0.264 (4 5) 0.798 (4 6)
-0.091 (5 6)
A=2
0.618 (1 2) 0.408 (1 3) 0.027 (1 4) 0.166 (1 5) 0.285 (1 6)
0.944 (2 3) 0.505 (2 4) 0.494 (2 5) 0.732 (2 6)
0.581 (3 4) 0.644 (3 5) 0.767 (3 6)
0.749 (4 5) 0.566 (4 6)
0.358 (5 6)
A=3
0.287 (1 2) 0.379 (1 3) -0.146 (1 4) 0.42 (1 5) 0.387 (1 6)
0.782 (2 3) 0.402 (2 4) 0.731 (2 5) 0.28 (2 6)
0.443 (3 4) 0.739 (3 5) 0.570 (3 6)
0.629 (4 5) 0.467 (4 6)
0.51 (5 6)
> table(sort(round(rr, 1)))
-0.1 0 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
2 1 1 6 10 6 7 5 4 3
1 1 1 2 2 3 4 5 6 7rr にはすべての相関が代入されています。相関の範囲は -0.1 から 0.9 までです。-0.1~ 0.2,0.3 ~ 0.5, 0.6 ~ 0.7,0.8 ~ 0.9 の 4つの範囲に分けることができそうです。4つの相関を仮定した Stan のモデル(7+4個のパラメータ)の WAIC値は 1546.8 まで下がりました。
4 chains, each with iter=10000; warmup=5000; thin=1; adapt_delta = 0.99;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 5% 50% 95% 97.5% n_eff Rhat
mu[1,1] 222.25 0.13 16.58 189.63 194.86 222.31 249.34 254.66 15222 1
mu[1,2] 90.05 0.13 15.40 60.02 64.72 89.96 115.14 120.45 13790 1
mu[1,3] 113.89 0.11 14.09 86.59 90.75 113.85 137.03 141.51 17229 1
mu[1,4] 137.21 0.11 13.84 110.06 114.52 137.14 159.85 164.40 17362 1
mu[1,5] 129.68 0.10 13.15 104.10 108.15 129.54 151.15 155.81 17857 1
mu[1,6] 137.21 0.11 13.84 110.06 114.52 137.14 159.85 164.40 17362 1
mu[2,1] 345.55 0.15 19.48 306.66 313.31 345.66 377.23 383.93 17365 1
mu[2,2] 266.53 0.17 21.53 223.98 231.31 266.49 301.64 308.87 15971 1
mu[2,3] 236.67 0.16 20.13 196.87 203.46 236.65 269.78 276.39 15064 1
mu[2,4] 189.51 0.15 18.96 152.28 158.33 189.34 220.39 226.69 16567 1
mu[2,5] 199.28 0.15 19.61 160.38 166.81 199.32 231.33 237.56 16306 1
mu[2,6] 189.51 0.15 18.96 152.28 158.33 189.34 220.39 226.69 16567 1
mu[3,1] 277.31 0.12 15.33 246.90 252.19 277.47 302.51 307.41 17702 1
mu[3,2] 91.93 0.12 15.56 61.28 66.21 91.89 117.25 122.15 17037 1
mu[3,3] 97.95 0.13 15.32 67.94 72.91 97.96 122.81 127.90 14107 1
mu[3,4] 121.79 0.10 13.07 96.10 100.30 121.74 143.21 147.62 17238 1
mu[3,5] 119.55 0.13 17.50 85.33 90.67 119.50 148.17 154.30 17703 1
mu[3,6] 121.79 0.10 13.07 96.10 100.30 121.74 143.21 147.62 17238 1
sigma 69.72 0.06 5.96 59.63 60.92 69.19 80.36 82.86 8489 1
rho[1] 0.09 0.00 0.14 -0.18 -0.14 0.08 0.33 0.38 6974 1
rho[2] 0.41 0.00 0.09 0.23 0.26 0.41 0.56 0.58 6208 1
rho[3] 0.61 0.00 0.06 0.49 0.51 0.62 0.72 0.73 6971 1
rho[4] 0.75 0.00 0.05 0.66 0.67 0.75 0.82 0.83 7313 1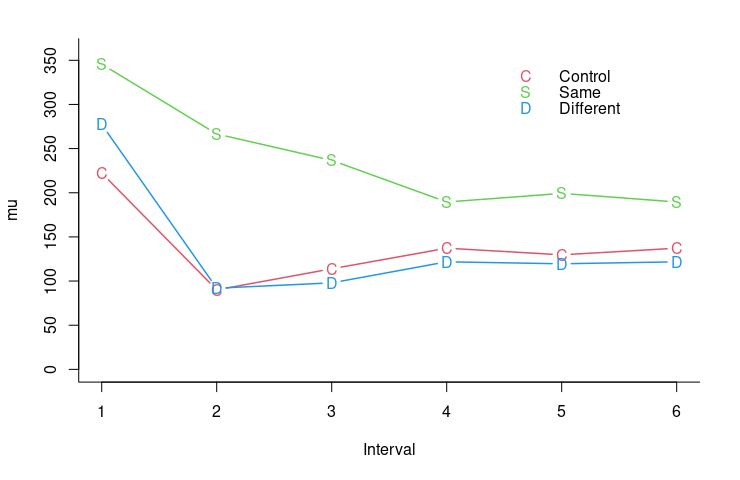
母平均の事後期待値とデータの平均値には若干のずれがありますが,全体のパターンは再現されています。
mean se_mean sd 2.5% 5% 50% 95% 97.5% n_eff Rhat
muT 171.54 0.08 10.34 151.52 154.74 171.47 188.77 192.21 16799 1
mA[1] -33.15 0.06 7.32 -47.79 -45.14 -33.18 -21.17 -18.78 16980 1
mA[2] 66.30 0.11 14.64 37.56 42.35 66.37 90.29 95.59 16980 1
mA[3] -33.15 0.06 7.32 -47.79 -45.14 -33.18 -21.17 -18.78 16980 1
mB[1] 110.17 0.07 8.11 94.15 96.84 110.20 123.51 126.19 13880 1
mB[2] -22.03 0.01 1.62 -25.24 -24.70 -22.04 -19.37 -18.83 13880 1
mB[3] -22.03 0.01 1.62 -25.24 -24.70 -22.04 -19.37 -18.83 13880 1
mB[4] -22.03 0.01 1.62 -25.24 -24.70 -22.04 -19.37 -18.83 13880 1
mB[5] -22.03 0.01 1.62 -25.24 -24.70 -22.04 -19.37 -18.83 13880 1
mB[6] -22.03 0.01 1.62 -25.24 -24.70 -22.04 -19.37 -18.83 13880 1
mAB[1,1] -26.30 0.06 6.09 -38.45 -36.31 -26.29 -16.37 -14.44 11332 1
mAB[1,2] -26.30 0.06 6.09 -38.45 -36.31 -26.29 -16.37 -14.44 11332 1
mAB[1,3] -2.46 0.06 6.76 -15.49 -13.56 -2.50 8.76 10.85 14123 1
mAB[1,4] 20.86 0.05 5.83 9.52 11.40 20.83 30.49 32.49 12983 1
mAB[1,5] 13.33 0.06 6.95 -0.22 1.92 13.30 24.74 27.02 15724 1
mAB[1,6] 20.86 0.05 5.83 9.52 11.40 20.83 30.49 32.49 12983 1
mAB[2,1] -2.46 0.06 6.76 -15.49 -13.56 -2.50 8.76 10.85 14123 1
mAB[2,2] 50.72 0.09 10.43 30.13 33.65 50.71 67.97 71.24 13317 1
mAB[2,3] 20.86 0.05 5.83 9.52 11.40 20.83 30.49 32.49 12983 1
mAB[2,4] -26.30 0.06 6.09 -38.45 -36.31 -26.29 -16.37 -14.44 11332 1
mAB[2,5] -16.53 0.06 7.82 -31.93 -29.25 -16.59 -3.49 -1.21 19673 1
mAB[2,6] -26.30 0.06 6.09 -38.45 -36.31 -26.29 -16.37 -14.44 11332 1
mAB[3,1] 28.76 0.06 7.11 14.77 17.07 28.75 40.42 42.84 13390 1
mAB[3,2] -24.42 0.06 8.35 -40.88 -38.21 -24.44 -10.47 -7.86 21591 1
mAB[3,3] -18.40 0.06 6.98 -32.18 -29.86 -18.38 -6.98 -4.67 13640 1
mAB[3,4] 5.44 0.05 5.68 -5.68 -3.80 5.41 14.83 16.53 13067 1
mAB[3,5] 3.20 0.07 9.66 -16.18 -12.94 3.31 18.90 22.03 21803 1
mAB[3,6] 5.44 0.05 5.68 -5.68 -3.80 5.41 14.83 16.53 13067 1muT,mA,mB,mAB の事後期待値と各パーセンタイルです。mAB[1, 1]~mAB[1, 5] と mAB[1, 6],mAB[2, 1]~mAB[2, 5] と mAB[1, 6],mAB[3, 1]~mAB[3, 5] と mAB[1, 6] には,4つの推定されたパラメータが代入されています。それら以外のところは制約に基づいて値が割り当てられています。たとえば,mu[1,6] の値は,muT+mA[1]+mB[6]+mAB[1, 6] です。mu[3, 6] の値は,muT+mA[3]+mB[6]+mAB[3, 6] になります。この場合,mA[1]=mA[3] ですから,mu[1, 6] と mu[3, 6] の差は mAB[1, 6] と mAB[3, 6] の差のみに依存します。
モデルでは,要因A と要因B については,それぞれ,1つのパラメータを仮定し,交互作用について 4つのパラメータを仮定しました。加えて,相関に関する 4つのパラメータと分散に関する 1つのパラメータを仮定しました。モデルが推測した各条件の平均値は実験結果の全体的なパターンをよく再現しているようです。要因A の水準2(同環境条件)では活動性が上昇し,水準1 と水準3(統制条件と異環境条件)では活動性が低下しています。これらは,同環境条件のラットが薬物への耐性を持つことと,統制条件と異環境条件における薬物の影響を示唆しています。観察期間である要因B については,水準1 では活動性が高く,水準2~6 では一様に活動性が低くなります。この傾向は水準2 以降に薬物の影響が現れることを示唆しています。
2つの要因の交互作用については,統制条件(要因A の水準1)において要因B の水準1 と 2 が活動性を下げる効果を示し,水準4 と 6 が活動性を上げる効果を示しました。異環境条件(要因A の水準3)では,要因B の水準1 が活動性を上げる効果を示し,水準2 と 3 が活動性を下げる効果を示しました。初期の段階(要因B の水準1~水準3)で活動性が下がるのは薬物の影響であると考えられます。一方,異環境条件(要因A の水準2)では要因B の水準2 と水準3 でむしろ活動性が上がる方向に効果が現れ,要因B の水準4~水準6 では活動性を下げる方向に効果が表れています。予想通り,同じ環境では耐性が条件反応として現れるが,環境が異なると耐性が現れにくい傾向が示唆されました。
混合計画の実験データはベイズ統計のモデルを使わなければ分析できないデータではありませんが,Stan と WAIC と組み合わせることで実験結果に関する独自の仮説を検討できる点が興味深いと思います。分散分析におけるコントラストの考え方(Bird, 2004; Rosenthal, Rosnow, Rubin, 2000)を応用して,各要因の効果に関するベイズモデルを作成することも可能でしょう。
Stan による計算では,パラメータの数が多くなるほど時間がかかったり,警告のメッセージが数多く表示されたりします。Stan は乱数の生成を行っていますので,乱数の初期値(random seed)を変更することで警告数が減少する場合があります(増加することありますが)。「Rejecting initial value:」については,パラメータの初期値を乱数から 0(init = 0) にすることで抑えることができます。また,Stan に渡す変数(refresh)の値を変えることで途中経過の表示頻度を調整できます。
2021年3月26日
2019年6月16日